《2025年实验班提优训练暑假衔接版八升九年级数学人教版》

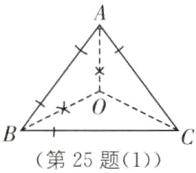
25. 中考新考法 类比猜想 (1)如图(1),作$\triangle ABC的两个内角\angle A$,$\angle B$的平分线,设交点为$O$,点$O在\angle C$的平分线上吗？试说明你的猜想,你又有什么新的发现？
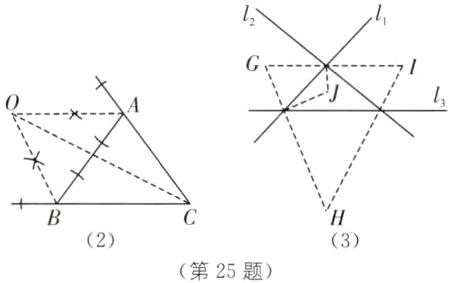
(2)如图(2),作$\triangle ABC的两个外角\angle BAE$,$\angle ABF$的平分线,设交点为$O$,点$O在\angle C$的平分线上吗？试说明你的猜想,你又有什么新的发现？
(3)你能用你的发现解决下面的实际问题吗？如图(3),直线$l_{1}$,$l_{2}$,$l_{3}$表示三条互相交叉的公路,现要建一个加油站,要使它到三条公路的距离相等,画出符合要求的点的位置,共有几个？

答案：

(1)如图
(1),点O在∠ACB的角平分线上.由此可得三角形的三条内角平分线相交于一点O，点O到三角形三条边的距离相等.
　
(2)如图
(2),点O在∠C的平分线上.由此可以得到点O到三角形三条边的距离相等.
　
(3)如图
(3),符合条件的点有4个:点G,H,I,J.

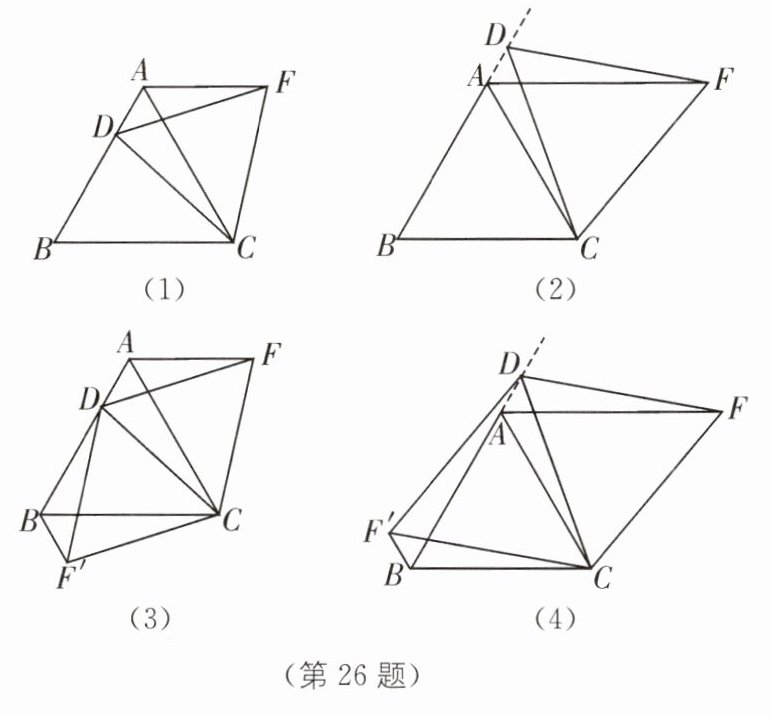
26. 中考新考法 操作探究 (1)操作发现：如图(1),$D是等边三角形ABC边BA$上一动点(点$D与点B$不重合),连接$DC$,以$DC为边在BC上方作等边三角形DCF$,连接$AF$。你能发现线段$AF与BD$之间的数量关系吗？并证明你发现的结论。
(2)类比猜想：如图(2),当动点$D运动至等边三角形ABC边BA$的延长线上时,其他作法与(1)相同,猜想$AF与BD$在(1)中的结论是否仍然成立？
(3)深入探究：
①如图(3),当动点$D在等边三角形ABC边BA$上运动时(点$D与点B$不重合),连接$DC$,以$DC为边在BC$上方、下方分别作等边三角形$DCF和等边三角形DCF'$,连接$AF$,$BF'$,探究$AF$,$BF'与AB$有何数量关系？并证明你探究的结论。
②如图(4),当动点$D在等边三角形ABC边BA$的延长线上运动时,其他作法与图(3)相同,①中的结论是否成立？若不成立,是否有新的结论？并证明你得出的结论。

答案：
(1)AF=BD.证明如下:
∵△ABC是等边三角形，
∴BC=AC、∠BCA=60°.
　同理可得DC=CF,∠DCF=60°.
∴∠BCA−∠DCA=∠DCF−∠DCA,即∠BCD=∠ACF.
　在△BCD和△ACF中,$\begin{cases} BC = AC, \\ ∠BCD = ∠ACF, \\ DC = FC, \end{cases}$
∴△BCD≌△ACF(SAS),
∴AF=BD.
(2)AF=BD仍然成立.证明如下:
∵△ABC是等边三角形，
∴BC=AC,∠BCA=60°.
　同理可得DC=CF,∠DCF=60°.
∴∠BCA+∠DCA=∠DCF+∠DCA,即∠BCD=∠ACF.
　在△BCD和△ACF中,$\begin{cases} BC = AC, \\ ∠BCD = ∠ACF, \\ DC = FC, \end{cases}$
∴△BCD≌△ACF(SAS).
∴AF=BD.
(3)①AF+BF'=AB.证明如下:
　由
(1)知△BCD≌△ACF(SAS),则BD=AF;
　同理可得△BCF'≌△ACD(SAS),则BF'=AD.
∴AF+BF'=BD+AD=AB.
　②①中的结论不成立.新的结论是AF=AB+BF'.证明如下:
　在△BCF'和△ACD中,$\begin{cases} BC = AC, \\ ∠BCF' = ∠ACD, \\ F'C = DC, \end{cases}$
∴△BCF'≌△ACD(SAS).
∴BF'=AD.
　由
(2)知AF=BD,
∴AF=BD=AB+AD=AB+BF',即AF=AB+BF'.