《2025年实验班提优训练暑假衔接版八升九年级数学人教版》

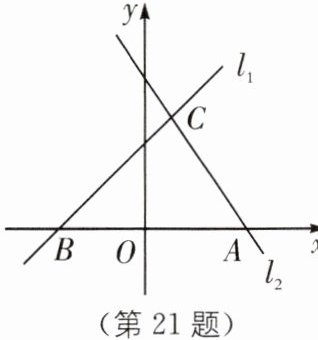
21. 如图,直线$l _ { 1 } : y = x + 3与过点A ( 3, 0 )的直线l _ { 2 }交于点C ( 1, m )$,与$x轴交于点B$.
(1)求直线$l _ { 2 }$的解析式；
(2)点$M在直线l _ { 1 }$上,$M N // y$轴,交直线$l _ { 2 }于点N$,若$M N = A B$,求点$M$的坐标.

答案：
(1)把x=1代入y=x+3，得y=4，
∴C(1,4)。设直线l₂的解析式为y=kx+b，
∴{k+b=4，3k+b=0，解得{k=-2，b=6，
∴直线l₂的解析式为y=-2x+6。
(2)在y=x+3中，令y=0，得x=-3，
∴B(-3,0)，
∴AB=3-(-3)=6。设M(a,a+3)，由MN//y轴，得N(a,-2a+6)，
∴MN=|a+3-(-2a+6)|=AB=6，解得a=3或a=-1，
∴M(3,6)或(-1,2)。

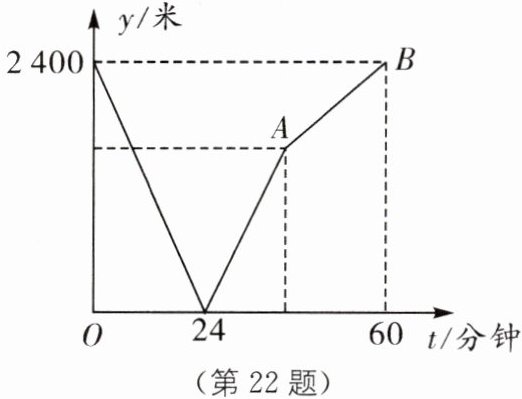
22. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地. 两人之间的距离$y$(米)与时间$t$(分钟)之间的函数关系如图所示.
(1)根据图象信息,当$t = $24分钟时,甲、乙两人相遇,甲的速度为40米/分钟；
(2)求出线段$A B$所表示的函数解析式.

由题意得，甲、乙速度和为$2400÷24 = 100$（米/分钟），乙的速度为$100 - 40=60$（米/分钟）。乙到达学校时间为$2400÷60 = 40$（分钟），此时甲行走路程为$40×40 = 1600$（米），故点$A$坐标为$(40,1600)$。设线段$AB$的函数解析式为$y=kt+b$，将$A(40,1600)$、$B(60,2400)$代入得$\begin{cases}40k + b=1600\\60k + b=2400\end{cases}$，解得$\begin{cases}k = 40\\b=0\end{cases}$，所以线段$AB$的函数解析式为$y = 40t(40\leq t\leq60)$。

答案：
(1)24；40
(2)由题意得，甲、乙速度和为$2400÷24 = 100$（米/分钟），乙的速度为$100 - 40=60$（米/分钟）。乙到达学校时间为$2400÷60 = 40$（分钟），此时甲行走路程为$40×40 = 1600$（米），故点$A$坐标为$(40,1600)$。设线段$AB$的函数解析式为$y=kt+b$，将$A(40,1600)$、$B(60,2400)$代入得$\begin{cases}40k + b=1600\\60k + b=2400\end{cases}$，解得$\begin{cases}k = 40\\b=0\end{cases}$，所以线段$AB$的函数解析式为$y = 40t(40\leq t\leq60)$。

23. 新情境 最佳消费方式选择 为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下：
普通消费：$35$元/次；
白金卡消费：购卡$280$元/张,凭卡免费消费$10次再送2$次；
钻石卡消费：购卡$560$元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身$6$次,他应选择哪种消费方式更合算?
(2)设一年内去该健身中心健身$x$次($x$为正整数),所需总费用为$y$元,请分别写出选择普通消费和白金卡消费的$y与x$的函数关系式.
(3)王阿姨每年去该健身中心健身至少$18$次,请通过计算帮助王阿姨选择最合算的消费方式.

答案：
(1)普通消费费用：$35×6 = 210$（元）
$210＜280＜560$，
∴选择普通消费方式更合算。
(2)普通消费：$y_{\text{普通}}=35x$
白金卡消费：
当$x\leq12$时，$y_{\text{白金卡}}=280$；
当$x＞12$时，$y_{\text{白金卡}}=280 + 35(x - 12)=35x - 140$
∴$y_{\text{白金卡}}=\begin{cases}280 & (x\leq12) \\ 35x - 140 & (x＞12)\end{cases}$
(3)当$x = 18$时：
$y_{\text{普通}}=35×18 = 630$，
$y_{\text{白金卡}}=35×18 - 140 = 490$
令$y_{\text{白金卡}}=560$，即$35x - 140 = 560$，解得$x = 20$
当$18\leq x\leq19$时，选择白金卡；
当$x = 20$时，白金卡和钻石卡费用相同；
当$x\geq21$时，选择钻石卡。