《2025年实验班提优训练暑假衔接版八升九年级数学人教版》

11. 下面几组数：① 7,8,9；② 12,9,15；③ $ m ^ { 2 } + n ^ { 2 } $,$ m ^ { 2 } - n ^ { 2 } $,$ 2 m n $($ m $,$ n $ 均为正整数,$ m ＞ n $)；④ $ a ^ { 2 } $,$ a ^ { 2 } + 1 $,$ a ^ { 2 } + 2 $. 其中能组成直角三角形的三边长的是②③.

答案： 1. 首先判断①：
对于$7$，$8$，$9$，根据勾股定理逆定理$a^{2}+b^{2}=c^{2}$（$c$为最长边）。
计算$7^{2}+8^{2}=49 + 64=113$，$9^{2}=81$，因为$113\neq81$，所以$7$，$8$，$9$不能组成直角三角形。
2. 然后判断②：
对于$12$，$9$，$15$，其中$15$是最长边。
计算$9^{2}+12^{2}=81 + 144 = 225$，$15^{2}=225$，即$9^{2}+12^{2}=15^{2}$，所以$12$，$9$，$15$能组成直角三角形。
3. 接着判断③：
对于$m^{2}+n^{2}$，$m^{2}-n^{2}$，$2mn$（$m$，$n$均为正整数，$m\gt n$），$(m^{2}-n^{2})^{2}+(2mn)^{2}$。
根据完全平方公式$(a - b)^{2}=a^{2}-2ab + b^{2}$和$(ab)^{2}=a^{2}b^{2}$展开：
$(m^{2}-n^{2})^{2}+(2mn)^{2}=m^{4}-2m^{2}n^{2}+n^{4}+4m^{2}n^{2}$。
合并同类项得$m^{4}+2m^{2}n^{2}+n^{4}=(m^{2}+n^{2})^{2}$，所以$m^{2}+n^{2}$，$m^{2}-n^{2}$，$2mn$能组成直角三角形。
4. 最后判断④：
对于$a^{2}$，$a^{2}+1$，$a^{2}+2$，$a^{2}+2$是最长边。
计算$(a^{2})^{2}+(a^{2}+1)^{2}=a^{4}+a^{4}+2a^{2}+1 = 2a^{4}+2a^{2}+1$，$(a^{2}+2)^{2}=a^{4}+4a^{2}+4$。
假设$2a^{4}+2a^{2}+1=a^{4}+4a^{2}+4$，即$a^{4}-2a^{2}-3 = 0$，令$t = a^{2}(t\geq0)$，则$t^{2}-2t - 3 = 0$，分解因式得$(t - 3)(t + 1)=0$，解得$t = 3$或$t=-1$（舍去），当$a^{2}=3$时$(a^{2})^{2}+(a^{2}+1)^{2}=(a^{2}+2)^{2}$，但不是对任意$a$都成立。
例如当$a = 1$时，$a^{2}=1$，$a^{2}+1 = 2$，$a^{2}+2 = 3$，$1^{2}+2^{2}=1 + 4 = 5\neq9 = 3^{2}$，所以$a^{2}$，$a^{2}+1$，$a^{2}+2$不能组成直角三角形。
综上，能组成直角三角形三边长的是②③。

12. 在 $ \triangle A B C $ 中,$ \angle C = 90 ^ { \circ } $,$ A B = 5 $,则 $ A B ^ { 2 } + A C ^ { 2 } + B C ^ { 2 } = $50.

答案： 50

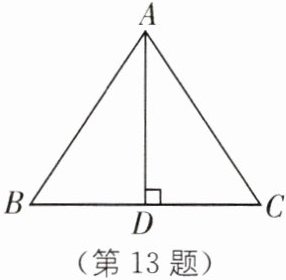
13. 如图,在等腰三角形 $ A B C $ 中,$ A B = A C $,$ A D $ 是底边上的高. 若 $ A B = 5 \mathrm { cm } $,$ B C = 6 \mathrm { cm } $,则 $ A D = $4 $ \mathrm { cm } $.

答案： 4

14. 已知 $ C D $ 是 $ \triangle A B C $ 的边 $ A B $ 上的高,若 $ C D = \sqrt { 3 } $,$ A D = 1 $,$ A B = 2 A C $,则 $ B C $ 的长为$2\sqrt{7}$或$2\sqrt{3}$.

答案： $2\sqrt{7}$或$2\sqrt{3}$

15. 如图,在 $ \triangle A B C $ 中,$ A B = 17 $,$ A C = 10 $,边 $ B C $ 的高 $ A D = 8 $,则边 $ B C $ 的长为21.

答案： 21

16. 如图,$ O $ 为数轴原点,$ A $,$ B $ 两点分别对应 $ - 3 $,3,作腰长为 4 的等腰 $ \triangle A B C $,连接 $ O C $,以 $ O $ 为圆心,$ C O $ 长为半径画弧交数轴于点 $ M $,则点 $ M $ 对应的实数为$\sqrt{7}$.

答案： $\sqrt{7}$

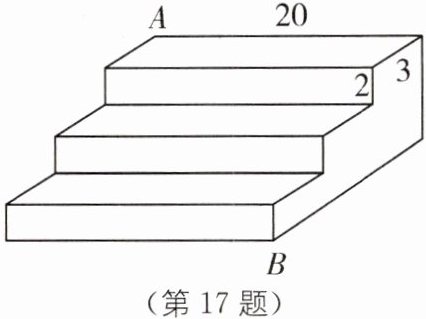
17. 如图,一个三级台阶,它的每一级的长、宽和高分别为 20,3,2,$ A $ 和 $ B $ 是这个台阶两个相对的端点,点 $ A $ 有一只蚂蚁,想到点 $ B $ 去吃可口的食物,那么蚂蚁沿着台阶面爬到点 $ B $ 最短路程是______25.

答案： 25

18. 在数轴上作出表示 $ \sqrt { 29 } $ 的点.

答案：

19. 如图,在 $ \triangle A B C $ 中,$ A D $ 是边 $ B C $ 上的高,$ A B = 15 \mathrm { cm } $,$ A C = 13 \mathrm { cm } $,$ A D = 12 \mathrm { cm } $,求 $ \triangle A B C $ 的面积.

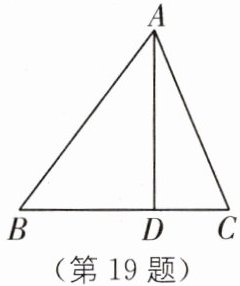
答案：
∵AD是边BC上的高,
∴∠ADB=∠ADC=90°,
∴BD²=AB²-AD²=81 cm²,CD²=AC²-AD²=25 cm²,
∴BD=9 cm,CD=5 cm，
∴BC=BD+DC=14 cm，
∴S△ABC= $\frac{1}{2}$BC·AD= $\frac{1}{2}$×14×12=84(cm²).

20. 我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察：3,4,5；5,12,13；7,24,25；9,40,41；…,发现这些勾股数的勾都是奇数,且从 3 起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数：11,60,61；
(2)若第一个数用字母 $ n $($ n $ 为奇数,且 $ n \geqslant 3 $)表示,那么后两个数用含 $ n $ 的代数式分别表示为$\frac{n^2-1}{2}$和$\frac{n^2+1}{2}$,请用所学知识说明它们是一组勾股数.
证明如下：
∵n²+$(\frac{n^2-1}{2})^2$=n²+$\frac{n^4-2n^2+1}{4}$=$\frac{n^4+2n^2+1}{4}$，
$(\frac{n^2+1}{2})^2$=$\frac{n^4+2n^2+1}{4}$，
∴n²+$(\frac{n^2-1}{2})^2$=$(\frac{n^2+1}{2})^2$.
又n≥3,且n为奇数,∴由n,$\frac{n^2-1}{2}$,$\frac{n^2+1}{2}$三个数组成的数是勾股数.

答案：
(1)11,60,61；
(2)$\frac{n^2-1}{2}$ $\frac{n^2+1}{2}$ 证明如下：
∵n²+$(\frac{n^2-1}{2})^2$=n²+$\frac{n^4-2n^2+1}{4}$=$\frac{n^4+2n^2+1}{4}$，
$(\frac{n^2+1}{2})^2$=$\frac{n^4+2n^2+1}{4}$，
∴n²+$(\frac{n^2-1}{2})^2$=$(\frac{n^2+1}{2})^2$.
又n≥3,且n为奇数,
∴由n,$\frac{n^2-1}{2}$,$\frac{n^2+1}{2}$三个数组成的数是勾股数.