《2025年实验班提优训练暑假衔接版八升九年级数学人教版》

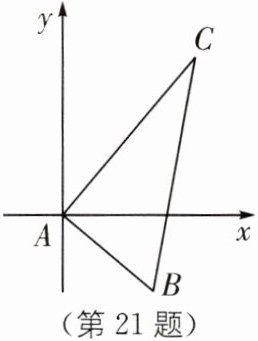
21. 如图,甲、乙两船从港口 $ A $ 同时出发,甲船以 16 海里/时的速度向北偏东 $ 40 ^ { \circ } $ 航行,乙船向南偏东 $ 50 ^ { \circ } $ 航行,3 小时后,甲船到达 $ C $ 岛,乙船到达 $ B $ 岛. 若 $ C $,$ B $ 两岛相距 60 海里,问乙船的航速是多少？

答案： 12海里/时

22. 小东拿着一根长竹竿进一个宽为 $ 3 \mathrm { m } $ 的城门,他先横着拿不进去,又竖起来拿,结果竿比城门高 1 米,当他把竿斜着时,两端刚好顶着城门的对角,问竿长多少米？

答案： 设城门高为x米,则竿长为(x+1)米，
依题意,得3²+x²=(x+1)²,解得x=4,故竿长为5米.

23. 中考新考法 归纳一般结论 在 $ \triangle A B C $ 中,$ B C = a $,$ A C = b $,$ A B = c $,设 $ c $ 为最长边,当 $ a ^ { 2 } + b ^ { 2 } = c ^ { 2 } $ 时,$ \triangle A B C $ 是直角三角形；当 $ a ^ { 2 } + b ^ { 2 } \neq c ^ { 2 } $ 时,利用代数式 $ a ^ { 2 } + b ^ { 2 } $ 和 $ c ^ { 2 } $ 的大小关系,探究 $ \triangle A B C $ 的形状(按角分类).
(1)当 $ \triangle A B C $ 三边分别为 6,8,9 时,$ \triangle A B C $ 为锐角三角形；当 $ \triangle A B C $ 三边分别为 6,8,11 时,$ \triangle A B C $ 为钝角三角形；
(2)猜想,当 $ a ^ { 2 } + b ^ { 2 } $＞$ c ^ { 2 } $ 时,$ \triangle A B C $ 为锐角三角形；当 $ a ^ { 2 } + b ^ { 2 } $＜$ c ^ { 2 } $ 时,$ \triangle A B C $ 为钝角三角形；
(3)判断当 $ a = 2 $,$ b = 4 $ 时,$ \triangle A B C $ 的形状,并求出对应的 $ c $ 的取值范围.
∵c为最长边,2+4=6,∴4≤c＜6.
a²+b²=2²+4²=20.
①a²+b²＞c²,即c²＜20,0＜c＜$2\sqrt{5}$，
∴当4≤c＜$2\sqrt{5}$时,这个三角形是锐角三角形.
②a²+b²=c²,即c²=20,c=$2\sqrt{5}$，
∴当c=$2\sqrt{5}$时,这个三角形是直角三角形.
③a²+b²＜c²,即c²＞20,c＞$2\sqrt{5}$，
∴当$2\sqrt{5}$＜c＜6时,这个三角形是钝角三角形.

答案：
(1)锐角 钝角；
(2)＞ ＜；
(3)
∵c为最长边,2+4=6,
∴4≤c＜6.
a²+b²=2²+4²=20.
①a²+b²＞c²,即c²＜20,0＜c＜$2\sqrt{5}$，
∴当4≤c＜$2\sqrt{5}$时,这个三角形是锐角三角形.
②a²+b²=c²,即c²=20,c=$2\sqrt{5}$，
∴当c=$2\sqrt{5}$时,这个三角形是直角三角形.
③a²+b²＜c²,即c²＞20,c＞$2\sqrt{5}$，
∴当$2\sqrt{5}$＜c＜6时,这个三角形是钝角三角形.