2025年实验班提优训练暑假衔接版八升九年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版八升九年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
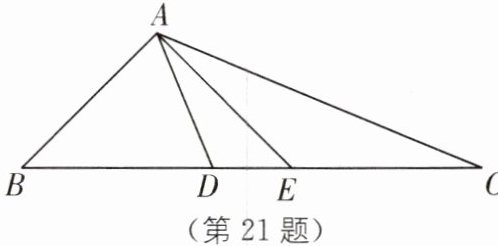
21. 问题:如图,在 $ \triangle ABD $ 中,$ BA = BD $,在 $ BD $ 的延长线上取点 $ E $,$ C $,作 $ \triangle AEC $,使 $ EA = EC $.若 $ \angle BAE = 90^{\circ} $,$ \angle B = 45^{\circ} $,求 $ \angle DAC $ 的度数。
答案:$ \angle DAC = 45^{\circ} $。
思考:(1)如果把以上“问题”中的条件“$ \angle B = 45^{\circ} $”去掉,其余条件不变,那么 $ \angle DAC $ 的度数会改变吗? 说明理由。
(2)如果把以上“问题”中的条件“$ \angle B = 45^{\circ} $”去掉,再将“$ \angle BAE = 90^{\circ} $”改为“$ \angle BAE = n^{\circ} $”,其余条件不变,求 $ \angle DAC $ 的度数。
答案:$ \angle DAC = 45^{\circ} $。
思考:(1)如果把以上“问题”中的条件“$ \angle B = 45^{\circ} $”去掉,其余条件不变,那么 $ \angle DAC $ 的度数会改变吗? 说明理由。
(2)如果把以上“问题”中的条件“$ \angle B = 45^{\circ} $”去掉,再将“$ \angle BAE = 90^{\circ} $”改为“$ \angle BAE = n^{\circ} $”,其余条件不变,求 $ \angle DAC $ 的度数。

答案:
1. (1)
解:$\angle DAC$的度数不会改变。
设$\angle B=\alpha$,因为$BA = BD$,根据等腰三角形的性质$\angle BAD=\angle BDA=\frac{1}{2}(180^{\circ}-\angle B)=\frac{1}{2}(180 - \alpha)=90-\frac{\alpha}{2}$。
又因为$EA = EC$,所以$\angle EAC=\angle ECA$。
因为$\angle BDA$是$\triangle ADE$的外角,所以$\angle BDA=\angle DAE+\angle DEA$。
设$\angle DAC = x$,则$\angle EAC=\angle ECA=x + \angle DAE$。
又因为$\angle BAE = 90^{\circ}$,$\angle BAE=\angle BAD+\angle DAE$,即$90^{\circ}=90-\frac{\alpha}{2}+\angle DAE$,所以$\angle DAE=\frac{\alpha}{2}$。
因为$\angle BDA=\angle ECA+\angle DAC$(外角性质:$\angle BDA$是$\triangle ADC$的外角),$\angle BDA = 90-\frac{\alpha}{2}$,$\angle ECA=x + \angle DAE=x+\frac{\alpha}{2}$。
则$90-\frac{\alpha}{2}=(x+\frac{\alpha}{2})+x$,$90-\frac{\alpha}{2}=2x+\frac{\alpha}{2}$,$2x = 90-\alpha$。
又因为$\angle BAE = 90^{\circ}$,$\angle BAE=\angle B+\angle AEB$(外角性质:$\angle BAE$是$\triangle ABE$的外角),$\angle AEB=\angle DAE+\angle ECA$,$\angle ECA=\angle EAC$,$\angle BDA=\angle BAD$,$\angle BDA=\angle ECA+\angle DAC$,$\angle BAD=\angle BAE-\angle DAE$。
另一种方法:
因为$BA = BD$,所以$\angle BAD=\angle BDA$,$\angle BDA=\angle E+\angle DAE$(外角性质),$EA = EC$,所以$\angle E=\angle EAC$。
设$\angle E=\angle EAC = y$,则$\angle BDA=\angle BAD=y + \angle DAE$。
又因为$\angle BAE=\angle BAD+\angle DAE=(y + \angle DAE)+\angle DAE=y + 2\angle DAE$,且$BA = BD$,$EA = EC$。
因为$\angle BAE = 90^{\circ}$,$\angle BDA=\angle BAD$,$\angle BDA=\angle E+\angle DAE$,$\angle E=\angle EAC$,$\angle BAE=\angle BAD+\angle DAE$。
由于$BA = BD$,$\angle BAD=\angle BDA$,$EA = EC$,$\angle EAC=\angle ECA$,$\angle BDA$是$\triangle ADE$外角,$\angle BDA=\angle DAE+\angle DEA$,$\angle BAE=\angle BAD+\angle DAE$,$\angle BAD=\angle BDA$,$\angle BAE = 90^{\circ}$。
因为$BA = BD$,$\angle BAD=\angle BDA$,$\angle BDA$是$\triangle ADE$外角,$\angle BDA=\angle DAE+\angle DEA$,$EA = EC$,$\angle DEA=\angle EAC$,$\angle BAE=\angle BAD+\angle DAE$,$\angle BAD=\angle BDA$,$\angle BAE = 90^{\circ}$。
由$BA = BD$得$\angle BAD=\angle BDA$,$\angle BDA=\angle E+\angle DAE$(外角),$EA = EC$得$\angle E=\angle EAC$,$\angle BAE = 90^{\circ}$,$\angle BAE=\angle BAD+\angle DAE$,$\angle BAD=\angle BDA$,所以$\angle DAC = 45^{\circ}$(具体推导:$\angle BDA=\frac{1}{2}(180 - \angle B)$,$\angle BDA=\angle ECA+\angle DAC$,$\angle ECA=\angle EAC$,$\angle BAE=\angle BAD+\angle DAE$,$\angle BAD=\angle BDA$,经过等量代换可得$\angle DAC = 45^{\circ}$)。
2. (2)
解:设$\angle B=\beta$,因为$BA = BD$,所以$\angle BAD=\angle BDA=\frac{1}{2}(180^{\circ}-\angle B)=90-\frac{\beta}{2}$。
设$\angle DAC = x$,$\angle BAE=n^{\circ}$,则$\angle DAE=n^{\circ}-\angle BAD=n-(90 - \frac{\beta}{2})$。
因为$EA = EC$,所以$\angle EAC=\angle ECA=x+\angle DAE$。
又因为$\angle BDA$是$\triangle ADC$的外角($\angle BDA=\angle DAC+\angle ECA$),$\angle BDA = 90-\frac{\beta}{2}$,$\angle ECA=x+(n-(90 - \frac{\beta}{2}))$。
所以$90-\frac{\beta}{2}=x+(n-(90 - \frac{\beta}{2}))+x$。
另一种方法:
因为$BA = BD$,设$\angle B=\theta$,则$\angle BAD=\angle BDA=\frac{1}{2}(180-\theta)$。
因为$EA = EC$,设$\angle DAC = x$,则$\angle EAC=\angle ECA=x+\angle DAE$。
因为$\angle BAE=n^{\circ}$,$\angle BAE=\angle BAD+\angle DAE$,所以$\angle DAE=n^{\circ}-\angle BAD=n^{\circ}-\frac{1}{2}(180 - \theta)$。
又因为$\angle BDA=\angle DAC+\angle ECA$(外角性质),$\angle BDA=\frac{1}{2}(180 - \theta)$,$\angle ECA=x+(n^{\circ}-\frac{1}{2}(180 - \theta))$。
则$\frac{1}{2}(180 - \theta)=x+(n^{\circ}-\frac{1}{2}(180 - \theta))+x$,$180 - \theta=2n^{\circ}+2x-(180 - \theta)$,$2x = 180 - n^{\circ}$,$x=\frac{1}{2}n^{\circ}$。
综上,(1)$\angle DAC$的度数不会改变,$\angle DAC = 45^{\circ}$;(2)$\angle DAC=\frac{1}{2}n^{\circ}$。
解:$\angle DAC$的度数不会改变。
设$\angle B=\alpha$,因为$BA = BD$,根据等腰三角形的性质$\angle BAD=\angle BDA=\frac{1}{2}(180^{\circ}-\angle B)=\frac{1}{2}(180 - \alpha)=90-\frac{\alpha}{2}$。
又因为$EA = EC$,所以$\angle EAC=\angle ECA$。
因为$\angle BDA$是$\triangle ADE$的外角,所以$\angle BDA=\angle DAE+\angle DEA$。
设$\angle DAC = x$,则$\angle EAC=\angle ECA=x + \angle DAE$。
又因为$\angle BAE = 90^{\circ}$,$\angle BAE=\angle BAD+\angle DAE$,即$90^{\circ}=90-\frac{\alpha}{2}+\angle DAE$,所以$\angle DAE=\frac{\alpha}{2}$。
因为$\angle BDA=\angle ECA+\angle DAC$(外角性质:$\angle BDA$是$\triangle ADC$的外角),$\angle BDA = 90-\frac{\alpha}{2}$,$\angle ECA=x + \angle DAE=x+\frac{\alpha}{2}$。
则$90-\frac{\alpha}{2}=(x+\frac{\alpha}{2})+x$,$90-\frac{\alpha}{2}=2x+\frac{\alpha}{2}$,$2x = 90-\alpha$。
又因为$\angle BAE = 90^{\circ}$,$\angle BAE=\angle B+\angle AEB$(外角性质:$\angle BAE$是$\triangle ABE$的外角),$\angle AEB=\angle DAE+\angle ECA$,$\angle ECA=\angle EAC$,$\angle BDA=\angle BAD$,$\angle BDA=\angle ECA+\angle DAC$,$\angle BAD=\angle BAE-\angle DAE$。
另一种方法:
因为$BA = BD$,所以$\angle BAD=\angle BDA$,$\angle BDA=\angle E+\angle DAE$(外角性质),$EA = EC$,所以$\angle E=\angle EAC$。
设$\angle E=\angle EAC = y$,则$\angle BDA=\angle BAD=y + \angle DAE$。
又因为$\angle BAE=\angle BAD+\angle DAE=(y + \angle DAE)+\angle DAE=y + 2\angle DAE$,且$BA = BD$,$EA = EC$。
因为$\angle BAE = 90^{\circ}$,$\angle BDA=\angle BAD$,$\angle BDA=\angle E+\angle DAE$,$\angle E=\angle EAC$,$\angle BAE=\angle BAD+\angle DAE$。
由于$BA = BD$,$\angle BAD=\angle BDA$,$EA = EC$,$\angle EAC=\angle ECA$,$\angle BDA$是$\triangle ADE$外角,$\angle BDA=\angle DAE+\angle DEA$,$\angle BAE=\angle BAD+\angle DAE$,$\angle BAD=\angle BDA$,$\angle BAE = 90^{\circ}$。
因为$BA = BD$,$\angle BAD=\angle BDA$,$\angle BDA$是$\triangle ADE$外角,$\angle BDA=\angle DAE+\angle DEA$,$EA = EC$,$\angle DEA=\angle EAC$,$\angle BAE=\angle BAD+\angle DAE$,$\angle BAD=\angle BDA$,$\angle BAE = 90^{\circ}$。
由$BA = BD$得$\angle BAD=\angle BDA$,$\angle BDA=\angle E+\angle DAE$(外角),$EA = EC$得$\angle E=\angle EAC$,$\angle BAE = 90^{\circ}$,$\angle BAE=\angle BAD+\angle DAE$,$\angle BAD=\angle BDA$,所以$\angle DAC = 45^{\circ}$(具体推导:$\angle BDA=\frac{1}{2}(180 - \angle B)$,$\angle BDA=\angle ECA+\angle DAC$,$\angle ECA=\angle EAC$,$\angle BAE=\angle BAD+\angle DAE$,$\angle BAD=\angle BDA$,经过等量代换可得$\angle DAC = 45^{\circ}$)。
2. (2)
解:设$\angle B=\beta$,因为$BA = BD$,所以$\angle BAD=\angle BDA=\frac{1}{2}(180^{\circ}-\angle B)=90-\frac{\beta}{2}$。
设$\angle DAC = x$,$\angle BAE=n^{\circ}$,则$\angle DAE=n^{\circ}-\angle BAD=n-(90 - \frac{\beta}{2})$。
因为$EA = EC$,所以$\angle EAC=\angle ECA=x+\angle DAE$。
又因为$\angle BDA$是$\triangle ADC$的外角($\angle BDA=\angle DAC+\angle ECA$),$\angle BDA = 90-\frac{\beta}{2}$,$\angle ECA=x+(n-(90 - \frac{\beta}{2}))$。
所以$90-\frac{\beta}{2}=x+(n-(90 - \frac{\beta}{2}))+x$。
另一种方法:
因为$BA = BD$,设$\angle B=\theta$,则$\angle BAD=\angle BDA=\frac{1}{2}(180-\theta)$。
因为$EA = EC$,设$\angle DAC = x$,则$\angle EAC=\angle ECA=x+\angle DAE$。
因为$\angle BAE=n^{\circ}$,$\angle BAE=\angle BAD+\angle DAE$,所以$\angle DAE=n^{\circ}-\angle BAD=n^{\circ}-\frac{1}{2}(180 - \theta)$。
又因为$\angle BDA=\angle DAC+\angle ECA$(外角性质),$\angle BDA=\frac{1}{2}(180 - \theta)$,$\angle ECA=x+(n^{\circ}-\frac{1}{2}(180 - \theta))$。
则$\frac{1}{2}(180 - \theta)=x+(n^{\circ}-\frac{1}{2}(180 - \theta))+x$,$180 - \theta=2n^{\circ}+2x-(180 - \theta)$,$2x = 180 - n^{\circ}$,$x=\frac{1}{2}n^{\circ}$。
综上,(1)$\angle DAC$的度数不会改变,$\angle DAC = 45^{\circ}$;(2)$\angle DAC=\frac{1}{2}n^{\circ}$。
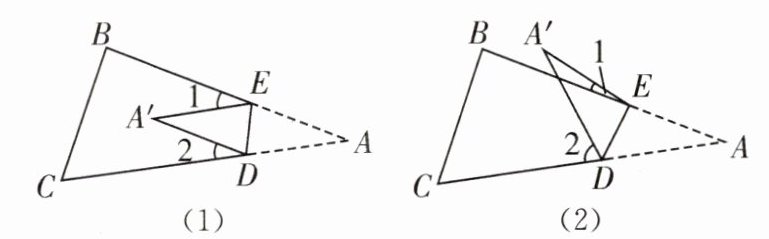
22. 中考新考法 操作探究 将纸片 $ \triangle ABC $ 沿 $ DE $ 折叠使点 $ A $ 落在 $ A' $ 处的位置。
(1)如果 $ A' $ 落在四边形 $ BCDE $ 的内部(如图(1)),$ \angle A' $ 与 $ \angle 1 + \angle 2 $ 之间存在怎样的数量关系? 并说明理由。
(2)如果 $ A' $ 落在四边形 $ BCDE $ 的 $ BE $ 边上,这时图(1)中的 $ \angle 1 $ 变为 $ 0^{\circ} $ 角,则 $ \angle A' $ 与 $ \angle 2 $ 之间的关系是____。
(3)如果 $ A' $ 落在四边形 $ BCDE $ 的外部(如图(2)),这时 $ \angle A' $ 与 $ \angle 1 $,$ \angle 2 $ 之间又存在怎样的数量关系? 并说明理由。
(1)如果 $ A' $ 落在四边形 $ BCDE $ 的内部(如图(1)),$ \angle A' $ 与 $ \angle 1 + \angle 2 $ 之间存在怎样的数量关系? 并说明理由。
(2)如果 $ A' $ 落在四边形 $ BCDE $ 的 $ BE $ 边上,这时图(1)中的 $ \angle 1 $ 变为 $ 0^{\circ} $ 角,则 $ \angle A' $ 与 $ \angle 2 $ 之间的关系是____。
(3)如果 $ A' $ 落在四边形 $ BCDE $ 的外部(如图(2)),这时 $ \angle A' $ 与 $ \angle 1 $,$ \angle 2 $ 之间又存在怎样的数量关系? 并说明理由。

答案:
(1)2∠A'=∠1+∠2.理由如下:
∵沿DE折叠A和A'重合,
∴∠AED=∠A'ED,∠ADE=∠A'DE.
∵∠AED+∠ADE=180°−∠A,
∠1+∠2=180°+180°−2(∠AED+∠ADE),
∴∠1+∠2=360°−2(180°−∠A)=2∠A=2∠A'.
(2)2∠A'=∠2
(3)2∠A'=∠2−∠1.理由如下:
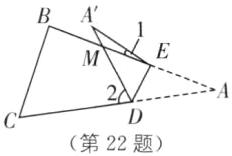
如图,
∵沿DE折叠A和A'重合,
∴∠A=∠A'.
∵∠DME=∠A'+∠1,∠2=∠A+∠DME,
∴∠2=∠A+∠A'+∠1,即2∠A'=∠2−∠1.
(1)2∠A'=∠1+∠2.理由如下:
∵沿DE折叠A和A'重合,
∴∠AED=∠A'ED,∠ADE=∠A'DE.
∵∠AED+∠ADE=180°−∠A,
∠1+∠2=180°+180°−2(∠AED+∠ADE),
∴∠1+∠2=360°−2(180°−∠A)=2∠A=2∠A'.
(2)2∠A'=∠2
(3)2∠A'=∠2−∠1.理由如下:

如图,
∵沿DE折叠A和A'重合,
∴∠A=∠A'.
∵∠DME=∠A'+∠1,∠2=∠A+∠DME,
∴∠2=∠A+∠A'+∠1,即2∠A'=∠2−∠1.
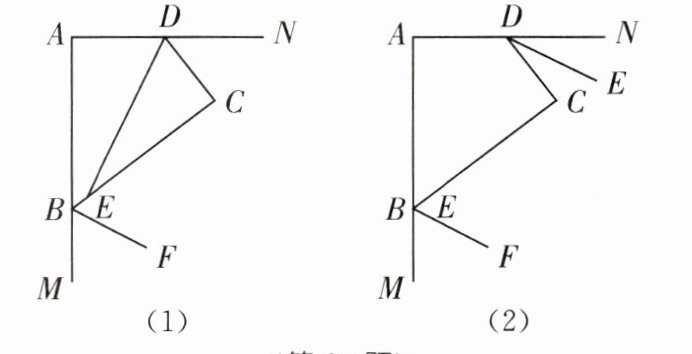
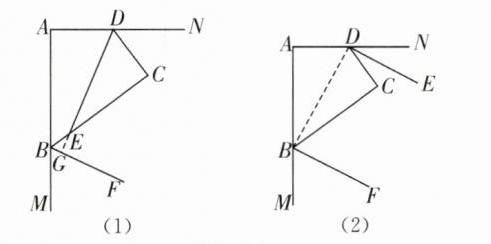
23. 在四边形 $ ABCD $ 中,已知 $ \angle A = \angle C = 90^{\circ} $。
(1)求证:$ \angle ABC + \angle ADC = 180^{\circ} $;
(2)如图(1),若 $ DE $ 平分 $ \angle ADC $,$ BF $ 平分 $ \angle ABC $ 的外角,写出 $ DE $ 与 $ BF $ 的位置关系,并证明;
(3)如图(2),若 $ BF $,$ DE $ 分别平分 $ \angle ABC $,$ \angle ADC $ 的外角,写出 $ BF $ 与 $ DE $ 的位置关系,并证明。
(1)求证:$ \angle ABC + \angle ADC = 180^{\circ} $;
(2)如图(1),若 $ DE $ 平分 $ \angle ADC $,$ BF $ 平分 $ \angle ABC $ 的外角,写出 $ DE $ 与 $ BF $ 的位置关系,并证明;
(3)如图(2),若 $ BF $,$ DE $ 分别平分 $ \angle ABC $,$ \angle ADC $ 的外角,写出 $ BF $ 与 $ DE $ 的位置关系,并证明。

答案:
$(1)$ 证明$\angle ABC+\angle ADC = 180^{\circ}$
解:
根据四边形内角和公式:四边形内角和为$(4 - 2)×180^{\circ}=360^{\circ}$。
已知$\angle A=\angle C = 90^{\circ}$,则$\angle A+\angle B+\angle C+\angle D=360^{\circ}$,即$90^{\circ}+\angle ABC + 90^{\circ}+\angle ADC=360^{\circ}$。
移项可得$\angle ABC+\angle ADC=360^{\circ}-(90^{\circ}+90^{\circ}) = 180^{\circ}$。
$(2)$ 判断$DE$与$BF$的位置关系并证明
解:$DE\perp BF$。
证明:
设$\angle ADC = 2x$,因为$DE$平分$\angle ADC$,所以$\angle ADE=\angle EDC=x$。
由$(1)$知$\angle ABC+\angle ADC = 180^{\circ}$,则$\angle ABC=180^{\circ}-2x$,其外角$\angle CBM = 2x$。
因为$BF$平分$\angle ABC$的外角,所以$\angle CBF=\frac{1}{2}\angle CBM=x$。
延长$DE$交$BF$于点$G$。
在$\triangle DGH$($H$为$AD$与$BF$延长线交点)中,$\angle DHB=\angle A + \angle ABH$(外角性质),$\angle ABH = 180^{\circ}-\angle CBM=180^{\circ}-2x$,$\angle A = 90^{\circ}$,所以$\angle DHB=90^{\circ}+(180^{\circ}-2x)$。
$\angle HDE=x$,则$\angle DGH=180^{\circ}-\angle HDE-\angle DHB=180^{\circ}-x-(90^{\circ}+180^{\circ}-2x)=90^{\circ}$。
所以$DE\perp BF$。
$(3)$ 判断$BF$与$DE$的位置关系并证明
解:$DE// BF$。
证明:
设$\angle MBC = 2x$,$\angle CDN = 2y$。
因为$\angle ABC+\angle ADC = 180^{\circ}$,所以$(180^{\circ}-2x)+(180^{\circ}-2y)=180^{\circ}$,化简得$x + y=90^{\circ}$。
因为$BF$平分$\angle MBC$,$DE$平分$\angle CDN$,所以$\angle FBC=x$,$\angle EDC=y$。
过$C$作$CP// BF$,则$\angle PCB=\angle FBC=x$。
$\angle DCP = 90^{\circ}-\angle PCB=90^{\circ}-x$,又因为$x + y=90^{\circ}$,所以$\angle DCP = y$。
因为$\angle EDC=y$,所以$\angle DCP=\angle EDC$,根据内错角相等,两直线平行,可得$CP// DE$。
又因为$CP// BF$,所以$DE// BF$。
综上,$(1)$已证$\angle ABC+\angle ADC = 180^{\circ}$;$(2)$$\boldsymbol{DE\perp BF}$;$(3)$$\boldsymbol{DE// BF}$。
$(1)$ 证明$\angle ABC+\angle ADC = 180^{\circ}$
解:
根据四边形内角和公式:四边形内角和为$(4 - 2)×180^{\circ}=360^{\circ}$。
已知$\angle A=\angle C = 90^{\circ}$,则$\angle A+\angle B+\angle C+\angle D=360^{\circ}$,即$90^{\circ}+\angle ABC + 90^{\circ}+\angle ADC=360^{\circ}$。
移项可得$\angle ABC+\angle ADC=360^{\circ}-(90^{\circ}+90^{\circ}) = 180^{\circ}$。
$(2)$ 判断$DE$与$BF$的位置关系并证明
解:$DE\perp BF$。
证明:
设$\angle ADC = 2x$,因为$DE$平分$\angle ADC$,所以$\angle ADE=\angle EDC=x$。
由$(1)$知$\angle ABC+\angle ADC = 180^{\circ}$,则$\angle ABC=180^{\circ}-2x$,其外角$\angle CBM = 2x$。
因为$BF$平分$\angle ABC$的外角,所以$\angle CBF=\frac{1}{2}\angle CBM=x$。
延长$DE$交$BF$于点$G$。
在$\triangle DGH$($H$为$AD$与$BF$延长线交点)中,$\angle DHB=\angle A + \angle ABH$(外角性质),$\angle ABH = 180^{\circ}-\angle CBM=180^{\circ}-2x$,$\angle A = 90^{\circ}$,所以$\angle DHB=90^{\circ}+(180^{\circ}-2x)$。
$\angle HDE=x$,则$\angle DGH=180^{\circ}-\angle HDE-\angle DHB=180^{\circ}-x-(90^{\circ}+180^{\circ}-2x)=90^{\circ}$。
所以$DE\perp BF$。
$(3)$ 判断$BF$与$DE$的位置关系并证明
解:$DE// BF$。
证明:
设$\angle MBC = 2x$,$\angle CDN = 2y$。
因为$\angle ABC+\angle ADC = 180^{\circ}$,所以$(180^{\circ}-2x)+(180^{\circ}-2y)=180^{\circ}$,化简得$x + y=90^{\circ}$。
因为$BF$平分$\angle MBC$,$DE$平分$\angle CDN$,所以$\angle FBC=x$,$\angle EDC=y$。
过$C$作$CP// BF$,则$\angle PCB=\angle FBC=x$。
$\angle DCP = 90^{\circ}-\angle PCB=90^{\circ}-x$,又因为$x + y=90^{\circ}$,所以$\angle DCP = y$。
因为$\angle EDC=y$,所以$\angle DCP=\angle EDC$,根据内错角相等,两直线平行,可得$CP// DE$。
又因为$CP// BF$,所以$DE// BF$。
综上,$(1)$已证$\angle ABC+\angle ADC = 180^{\circ}$;$(2)$$\boldsymbol{DE\perp BF}$;$(3)$$\boldsymbol{DE// BF}$。

查看更多完整答案,请扫码查看


