2025年实验班提优训练暑假衔接版八升九年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版八升九年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 下列图形具有两条对称轴的是(
A.等边三角形
B.平行四边形
C.矩形
D.正方形
C
).A.等边三角形
B.平行四边形
C.矩形
D.正方形
答案:
C
2. 如图,在$\triangle ABC$中,$AB= AC$,$\angle A= 40^{\circ}$,$AB的垂直平分线交AB于点D$,交$AC于点E$,连接$BE$,则$\angle CBE$的度数为(
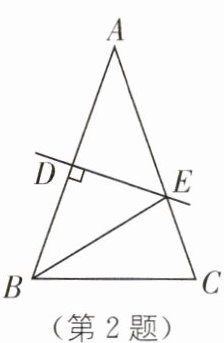
A.$70^{\circ}$
B.$80^{\circ}$
C.$40^{\circ}$
D.$30^{\circ}$
D
).
A.$70^{\circ}$
B.$80^{\circ}$
C.$40^{\circ}$
D.$30^{\circ}$
答案:
D
3. 如图,$C$表示灯塔,轮船从$A$处出发以每时30海里的速度向正北($AN$)方向航行,2小时后到达$B$处,测得$C在A的北偏东30^{\circ}$方向上,并在$B的北偏东60^{\circ}$方向上,那么$B处与灯塔C$之间的距离为(
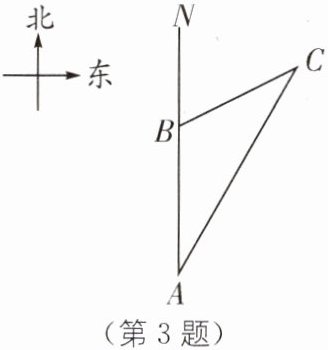
A.60海里
B.80海里
C.100海里
D.120海里
A
).
A.60海里
B.80海里
C.100海里
D.120海里
答案:
A
4. 某公路急转弯处设立了一面圆形大镜子,从镜子中看到的汽车车牌的部分号码如图所示,则该车牌的部分号码为(
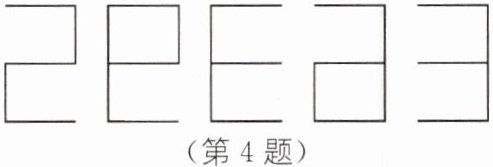
A.E9362
B.E9365
C.E6395
D.E6392
C
).
A.E9362
B.E9365
C.E6395
D.E6392
答案:
C
5. 在等腰三角形$ABC$中,腰$AB= 8$,底$BC= 5$,则这个三角形的周长为(
A.21
B.20
C.19
D.18
A
).A.21
B.20
C.19
D.18
答案:
A
6. 如图,$l// m$,等边三角形$ABC的顶点B在直线m$上,边$BC与直线m所夹锐角为20^{\circ}$,则$\angle \alpha$的度数为(
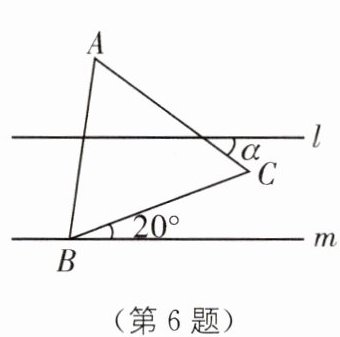
A.$60^{\circ}$
B.$45^{\circ}$
C.$40^{\circ}$
D.$30^{\circ}$
C
).
A.$60^{\circ}$
B.$45^{\circ}$
C.$40^{\circ}$
D.$30^{\circ}$
答案:
C
7. 已知点$A(a,2024)与点B(2025,b)关于x$轴对称,则$a+b$的值为(
A.$-1$
B.1
C.2
D.3
B
).A.$-1$
B.1
C.2
D.3
答案:
B
8. 如图,在$\triangle ABC$中,$AB= AC$,$\angle A= 36^{\circ}$,$BD$,$CE分别是\angle ABC$,$\angle BCD$的平分线,则图中的等腰三角形有(
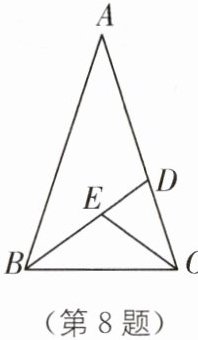
A.5个
B.4个
C.3个
D.2个
A
).
A.5个
B.4个
C.3个
D.2个
答案:
A
9. 在拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积. 如图是由5个边长为1的小正方形拼成的图形,$P$是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点$P$的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( ).
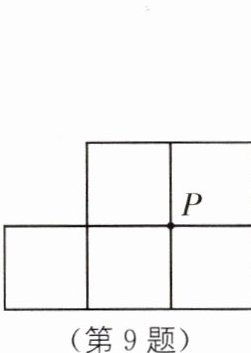
A.$2\sqrt{2}$
B.$\sqrt{5}$
C.$\frac{3\sqrt{5}}{2}$
D.$\sqrt{10}$

A.$2\sqrt{2}$
B.$\sqrt{5}$
C.$\frac{3\sqrt{5}}{2}$
D.$\sqrt{10}$
答案:
D [解析]本题考查了图形的分割问题,涉及到全等三角形、勾股定理等知识.如图,应当以沿过正方形ABCD的中心及点P的直线EF为裁剪线,过点F作FG⊥EM于点G.

∵EF将该图形分成了面积相等的两部分,
∴EF经过正方形ABCD对角线的交点,
∴AF=CN,BF=DN.
易证△PME≌△PDN,
∴EM=DN.
又AF=MG,
∴EG=EM+MG=DN+AF=DN+CN=DC=1.
在Rt△FGE中,EF=$\sqrt{FG^2+EG^2}$=$\sqrt{3^2+1^2}$=$\sqrt{10}$
故选D.
D [解析]本题考查了图形的分割问题,涉及到全等三角形、勾股定理等知识.如图,应当以沿过正方形ABCD的中心及点P的直线EF为裁剪线,过点F作FG⊥EM于点G.

∵EF将该图形分成了面积相等的两部分,
∴EF经过正方形ABCD对角线的交点,
∴AF=CN,BF=DN.
易证△PME≌△PDN,
∴EM=DN.
又AF=MG,
∴EG=EM+MG=DN+AF=DN+CN=DC=1.
在Rt△FGE中,EF=$\sqrt{FG^2+EG^2}$=$\sqrt{3^2+1^2}$=$\sqrt{10}$
故选D.
查看更多完整答案,请扫码查看


