《2025年实验班提优训练暑假衔接版八升九年级数学人教版》

24. (1)如图(1),若点 $ D $ 是 $ \triangle ABC $ 内任一点.求证:$ \angle D = \angle A + \angle ABD + \angle ACD $。
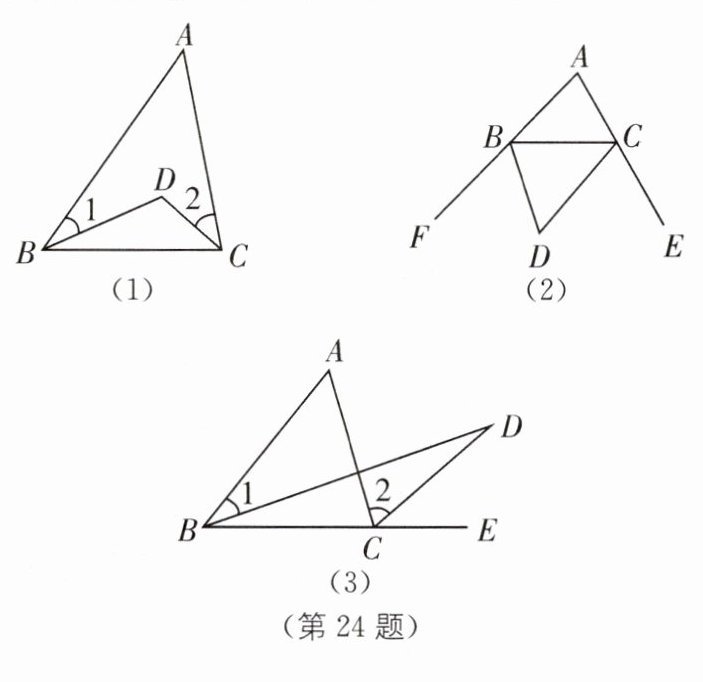
(2)若点 $ D $ 是 $ \triangle ABC $ 外一点,位置如图(2)所示.猜想 $ \angle D $,$ \angle A $,$ \angle ABD $,$ \angle ACD $ 有怎样的关系? 请直接写出所满足的解析式。(不需要证明)
(3)若点 $ D $ 是 $ \triangle ABC $ 外一点,位置如图(3)所示.猜想 $ \angle D $,$ \angle A $,$ \angle ABD $,$ \angle ACD $ 之间有怎样的关系,并证明你的结论。

答案：
(1)延长BD交AC于点E.
∵∠BDC是△CDE的外角，
∴∠BDC=∠2+∠CED.
∵∠CED是△ABE的外角，
∴∠CED=∠A+∠1.
∴∠BDC=∠A+∠1+∠2,
　　即∠D=∠A+∠ABD+∠ACD.
(2)∠D+∠A+∠ABD+∠ACD=360°.
(3)记BD与AC的交点为F,
∵∠AFD是△ABF的外角，
∴∠AFD=∠1+∠A.
∵∠AFD是△CDF的外角，
∴∠AFD=∠D+∠2.
∴∠A+∠1=∠D+∠2,
　　即∠A+∠ABD=∠D+∠ACD.

25. 中考新考法 新定义问题 数学概念
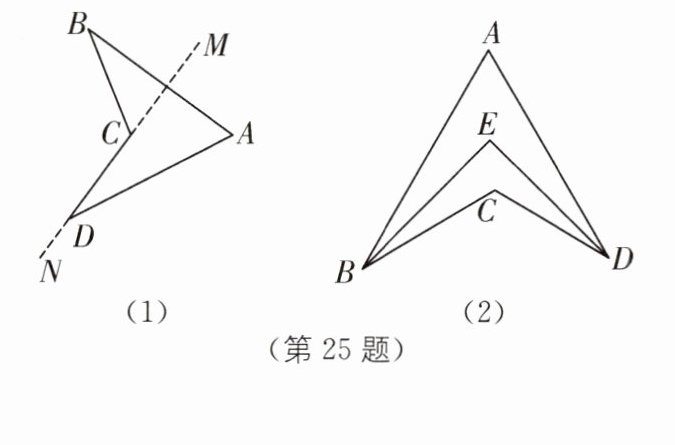
定义凹四边形:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边形叫做凹四边形。
如图(1),在四边形 $ ABCD $ 中,画出 $ DC $ 所在直线 $ MN $,边 $ BC $,$ AD $ 分别在直线 $ MN $ 的两旁,则四边形 $ ABCD $ 就是凹四边形。
性质初探
(1)在图(1)所示的凹四边形 $ ABCD $ 中,求证:$ \angle BCD = \angle A + \angle B + \angle D $。
深入研究
(2)如图(2),在凹四边形 $ ABCD $ 中,$ AB $ 与 $ CD $ 所在直线垂直,$ AD $ 与 $ BC $ 所在直线垂直,$ \angle ABC $,$ \angle ADC $ 的平分线相交于点 $ E $。
①求证:$ \angle A + \angle BCD = 180^{\circ} $。
②随着 $ \angle A $ 的变化,$ \angle BED $ 的大小会发生变化吗? 如果有变化,请探索 $ \angle BED $ 与 $ \angle A $ 的数量关系;如果没有变化,请求出 $ \angle BED $ 的度数。

答案：

(1)如图
(1),延长DC交AB于点E,
∵∠BEC是△AED的一个外角，
∴∠BEC=∠A+∠D.
　　同理,∠BCD=∠B+∠BEC,
∴∠BCD=∠A+∠B+∠D.
　　　
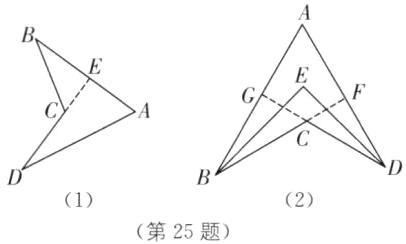
(2)①如图
(2),延长BC,DC分别交AD,AB于点F,G,
　　由题意可知,∠AFC=∠AGC=90°,
∵在四边形AFCG中,∠AFC+∠AGC+∠A+∠FCG=360°,
∴∠A+∠FCG=180°,
∵∠FCG=∠BCD,
∴∠A+∠BCD=180°.
　　②由
(1)可知，在凹四边形ABED中，
　　∠A+∠ABE+∠ADE=∠BED,Ⅰ
　　同理，在凹四边形EBCD中，
　　∠BED+∠EBC+∠EDC=∠BCD.Ⅱ
∵BE平分∠ABC,
∴∠ABE=∠EBC.同理,∠ADE=∠EDC,
∴Ⅰ-Ⅱ,得∠A+∠BCD=2∠BED,
　　由
(2)①可知,在凹四边形ABCD中,∠A+∠BCD =180°,
∴2∠BED=180°.
∴∠BED=90°.