《2025年实验班提优训练暑假衔接版八升九年级数学人教版》

21. 如图,在$\triangle ABC和\triangle DCE$中,$AC= DE$,$\angle B= \angle DCE= 90^{\circ}$,点$A$,$C$,$D$依次在同一条直线上,且$AB// DE$。
(1)求证：$\triangle ABC\cong\triangle DCE$；
(2)连接$AE$,当$BC= 5$,$AC= 12$时,求$AE$的长。

答案：
(1)
∵AB//DE,
∴∠BAC=∠D.
　又∠B=∠DCE=90°,AC=DE,
∴△ABC≌△DCE(AAS).
(2)
∵△ABC≌△DCE,
∴CE=BC=5.
∵∠ACE=90°,
∴AE=$\sqrt{AC^2 + CE^2}$=$\sqrt{25 + 144}$=13.

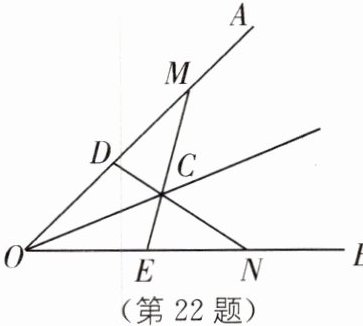
22. 如图,在$\angle AOB的两边OA$,$OB上分别取OM= ON$,$OD= OE$,$DN和EM相交于点C$。求证：点$C在\angle AOB$的平分线上。

答案：
∵OM=ON,OE=OD,∠MOE=∠NOD,
∴△MOE≌△NOD(SAS).
∴∠OME=∠OND.
　又OM=ON,OD=OE,
∴DM=EN.
　又∠DCM=∠ECN,
∴△MDC≌△NEC(AAS).
∴MC=NC.
∴△OMC≌△ONC(SSS).
∴∠MOC=∠NOC.
∴点C在∠AOB的平分线上.

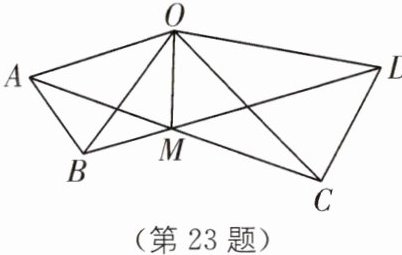
23. 如图,在$\triangle AOB和\triangle COD$中,$OA= OB$,$OC= OD$,$OA＜OC$,$\angle AOB= \angle COD= 36^{\circ}$。连接$AC$,$BD交于点M$,连接$OM$。
(1)求证：$AC= BD$；
(2)求$\angle AMB$的度数。

答案：
(1)
∵∠AOB=∠COD,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD.
　在△AOC和△BOD中,$\begin{cases} OA = OB, \\ ∠AOC = ∠BOD, \\ OC = OD, \end{cases}$
∴△AOC≌△BOD(SAS),
∴AC=BD.
(2)由
(1),可得∠OAC=∠OBD,
　由三角形外角的性质，得∠AMB + ∠OBD = ∠OAC + ∠AOB,
∴∠AMB=∠AOB=36°.

24. (1)如图(1),在$\triangle ABC$中,若$AB= 10$,$AC= 6$,则$BC边上的中线AD$长的取值范围是____；
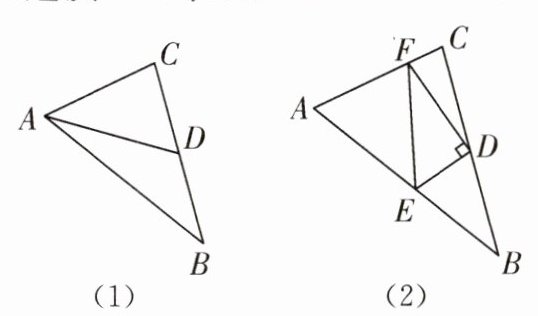
(2)如图(2),在$\triangle ABC$中,$D是边BC$上的中点,$DE\perp DF于点D$,$DE交AB于点E$,$DF交AC于点F$,连接$EF$,求证：$BE+CF＞EF$。.

答案：

(1)2＜AD＜8
(2)如图,延长FD至点G,使DG=DF,连接BG,EG.
　
∵点D是BC的中点，
∴DB=DC.
∵∠BDG=∠CDF,DG=DF,
∴△BDG≌△CDF.
∴BG=CF.
∵ED⊥FD,
∴∠EDF=∠EDG=90°.
　又ED=ED,FD=GD,
∴△EDF≌△EDG.
∴EF=EG.
∵在△BEG中,BE+BG＞EG,
∴BE+CF＞EF.