2025年实验班提优训练暑假衔接版八升九年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版八升九年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
11. 若式子$\frac{x}{\sqrt{2-x}}$有意义,则$x$的取值范围是
x<2
.
答案:
x<2
12. 当$1<x<3$时,$|1-x|+\sqrt{x^{2}-6x+9}= $
2
.
答案:
2
13. 如图,在矩形$ABCD$中,$AB= 8$,$BC= 4$,将矩形沿$AC$折叠,点$D落在点D'$处,则重叠部分$\triangle AFC$的面积为
10
.
答案:
10
14. 如图,公路$PQ和公路MN交于点P$,且$\angle NPQ= 30^{\circ}$,公路$PQ上有一所学校A$,$AP= 160\text{m}$,若有一拖拉机沿$MN方向以18\text{m/s}$的速度行驶并对学校产生影响,假设拖拉机行驶时周围$100\text{m}$以内会受到噪声的影响,则造成影响的时间为
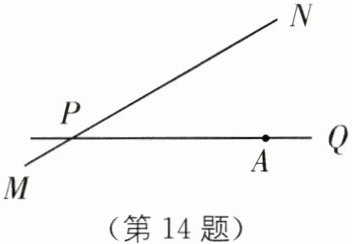
$\frac{20}{3}$
s.
答案:
$\frac{20}{3}$
15. 在四边形$ABCD$中,已知$AB// CD$,请补充一个条件
AB=CD或AD//BC(答案不唯一)
,使得四边形$ABCD$是平行四边形.
答案:
AB=CD或AD//BC(答案不唯一)
16. 如图,在菱形$ABCD$中,$AB= 4\text{cm}$,$\angle ADC= 120^{\circ}$,点$E$,$F同时由A$,$C$两点出发,分别沿$AB$,$CB方向向点B$匀速移动(到点$B$为止),点$E的速度为1\text{cm/s}$,点$F的速度为2\text{cm/s}$,经过$t\text{s}$,$\triangle DEF$为等边三角形,则$t$的值为
$\frac{4}{3}$
.
答案:
$\frac{4}{3}$
17. 如图,正方形$ABCD的对角线AC$,$BD相交于点O$,$\angle CAB的平分线交BD于点E$,交$BC于点F$. 若$OE= 1$,则$CF= $
2
.
答案:
2
18. 如图,一次函数$y= x+3的图象经过点P(a,b)$,$Q(c,d)$,则$a(c-d)-b(c-d)$的值为
9
.
答案:
9
19. 如图,正方形网格中的$\triangle ABC$,若小方格边长为1.
(1)求$\triangle ABC$的周长.
(2)$\triangle ABC$是直角三角形吗?为什么?
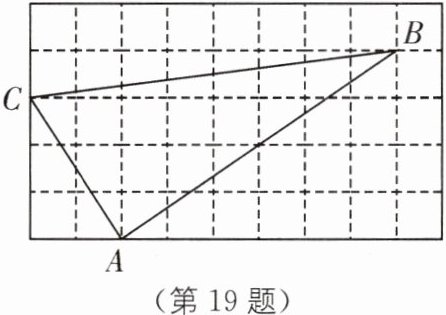
(1)求$\triangle ABC$的周长.
(2)$\triangle ABC$是直角三角形吗?为什么?

答案:
(1)由勾股定理,得AC=$\sqrt{3^2+2^2}=\sqrt{13}$,BC=$\sqrt{8^2+1^2}=\sqrt{65}$,AB=$\sqrt{6^2+4^2}=\sqrt{52}=2\sqrt{13}$.故△ABC的周长是$\sqrt{65}+3\sqrt{13}$.
(2)△ABC是直角三角形.理由如下:
∵AB²+AC²=(2$\sqrt{13}$)²+($\sqrt{13}$)²=65,BC²=($\sqrt{65}$)²=65,
∴AB²+AC²=BC².
∴△ABC是直角三角形.
(1)由勾股定理,得AC=$\sqrt{3^2+2^2}=\sqrt{13}$,BC=$\sqrt{8^2+1^2}=\sqrt{65}$,AB=$\sqrt{6^2+4^2}=\sqrt{52}=2\sqrt{13}$.故△ABC的周长是$\sqrt{65}+3\sqrt{13}$.
(2)△ABC是直角三角形.理由如下:
∵AB²+AC²=(2$\sqrt{13}$)²+($\sqrt{13}$)²=65,BC²=($\sqrt{65}$)²=65,
∴AB²+AC²=BC².
∴△ABC是直角三角形.
查看更多完整答案,请扫码查看


