《2025年实验班提优训练暑假衔接版八升九年级数学人教版》

1. 已知整数 $ x,y $ 满足 $ \sqrt{x}+2\sqrt{y}= \sqrt{50} $,那么整数对 $ (x,y) $ 共有(D)。
A.0 对
B.1 对
C.2 对
D.3 对

答案： D

2. 已知 $ b - a ＞ 0 $,且 $ a \geqslant 0 $,那么 $ \sqrt{a^{2}-2ab + b^{2}} - |a + b| $ 等于(C)。
A.0
B.$ -2b $
C.$ -2a $
D.不能化简

答案： C

3. 已知 $ a = \frac{1}{2 + \sqrt{3}} $,那么 $ \frac{a^{2} - 1}{a + 1} - \frac{\sqrt{a^{2} - 2a + 1}}{a^{2} - a} $ 的值等于(D)。
A.$ -1 - 2\sqrt{3} $
B.$ -1 $
C.$ 2 - \sqrt{3} $
D.3

答案： D

4. 代数式 $ \sqrt{x} + \sqrt{x - 1} + \sqrt{x - 2} $ 的最小值是(B)。
A.0
B.$ 1 + \sqrt{2} $
C.1
D.不存在

答案： B

5. 已知 $ a,b,c,d $ 为正数,$ a ＞ b ＞ c ＞ d $,记 $ x = \sqrt{(ab + cd)(a - b)(c - d)} $,$ y = \sqrt{(ac + bd)(a - c)(b - d)} $,$ z = \sqrt{(ad + bc)(a - d)(b - c)} $,则以 $ x,y,z $ 为边长(C)。
A.必可构成一个锐角三角形
B.必可构成一个钝角三角形
C.必可构成一个直角三角形
D.不一定构成三角形

答案： C

6. 已知 $ p,q $ 均为质数,且满足 $ 5p^{2} + 3q = 59 $,以 $ p + 3,1 - p + q,2p + q - 4 $ 为边长的三角形是(B)。
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形

答案： B

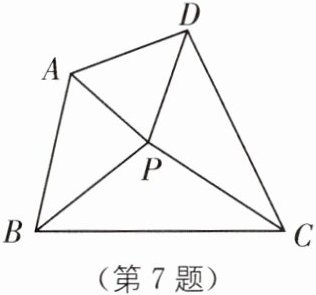
7. 如图,在四边形 $ ABCD $ 中,$ \angle A,\angle B,\angle C,\angle D $ 的内角平分线恰相交于一点 $ P $。记 $ \triangle APD,\triangle APB,\triangle BPC,\triangle DPC $ 的面积分别为 $ S_{1},S_{2},S_{3},S_{4} $,则有(A)。

A.$ S_{1} + S_{3} = S_{2} + S_{4} $
B.$ S_{1} + S_{2} = S_{3} + S_{4} $
C.$ S_{1} + S_{4} = S_{2} + S_{3} $
D.$ S_{1} + S_{3} \neq S_{2} + S_{4} $

答案： A

8. 如图,在等腰梯形 $ ABCD $ 中,$ AB // DC $,$ AB = 998 $,$ DC = 1001 $,$ AD = 1999 $,点 $ P $ 在线段 $ AD $ 上,则满足 $ \angle BPC = 90^{\circ} $ 的点 $ P $ 的个数为(C)。
A.0
B.1
C.2
D.不小于 3 的整数

答案： 1. 首先，以$AB$的中点$O$为原点，$AB$所在直线为$x$轴，$AB$的中垂线为$y$轴建立平面直角坐标系：
设$A(-\frac{998}{2},0)$，$B(\frac{998}{2},0)$，$D(-\frac{1001}{2},h)$，$C(\frac{1001}{2},h)$。
根据两点间距离公式$d = \sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$，由$AD = 1999$，可得$h=\sqrt{1999^{2}-\left(\frac{1001 - 998}{2}\right)^{2}}=\sqrt{1999^{2}-\left(\frac{3}{2}\right)^{2}}$。
设$P(x,0)$（因为$P$在$AD$上，$AD$在$x$轴下方，$y = 0$，设$A(-499,0)$，$B(499,0)$，$D(-500.5,h)$，$C(500.5,h)$，$AD$的方程：$y-0=\frac{h - 0}{-500.5 + 499}(x + 499)$，$P$点坐标设为$(x,0)$，$x\in[-500.5,-499]$。
由$\angle BPC = 90^{\circ}$，根据向量垂直的性质$\overrightarrow{PB}\cdot\overrightarrow{PC}=0$。
已知$\overrightarrow{PB}=(499 - x,0)$，$\overrightarrow{PC}=(500.5 - x,h)$，则$\overrightarrow{PB}\cdot\overrightarrow{PC}=(499 - x)(500.5 - x)=0$（这里用几何方法更简便）。
另一种方法：
以$BC$为直径作圆$O$，设$BC$的中点为$M$。
计算$BC$的长度：根据等腰梯形的性质，过$A$，$B$分别作$DC$的垂线，垂足为$E$，$F$。$DE=\frac{1001 - 998}{2}=\frac{3}{2}$，$AE=\sqrt{AD^{2}-DE^{2}}=\sqrt{1999^{2}-\left(\frac{3}{2}\right)^{2}}$，$BC = AD = 1999$，则圆$M$的半径$r=\frac{BC}{2}=\frac{1999}{2}$。
计算圆心$M$到$AD$的距离$d$：
设$AD$与$BC$所成角为$\theta$，$\cos\theta=\frac{AD^{2}+BC^{2}-(DC - AB)^{2}}{2AD\cdot BC}$（余弦定理，因为$AD = BC$），$\cos\theta=\frac{2×1999^{2}-3^{2}}{2×1999^{2}}$，$\sin\theta=\sqrt{1-\cos^{2}\theta}=\frac{3}{1999}$。
设$M$到$AD$的距离为$d$，根据梯形的性质，$d=\frac{1}{2}(AE + BF)$（$AE = BF$），$d=\frac{1}{2}\sqrt{1999^{2}-\left(\frac{3}{2}\right)^{2}}$。
比较$d$与$r$的大小：
$r=\frac{1999}{2}$，$d=\frac{1}{2}\sqrt{1999^{2}-\frac{9}{4}}$。
设$y_1 = r^{2}=\frac{1999^{2}}{4}$，$y_2=d^{2}=\frac{1999^{2}-\frac{9}{4}}{4}$，$r\gt d$。
2. 然后，根据圆与直线的位置关系：
以$BC$为直径的圆与$AD$的交点个数：
因为圆心到直线$AD$的距离$d\lt r$（$r$是圆的半径，$d$是圆心到直线$AD$的距离），所以直线$AD$与以$BC$为直径的圆有两个交点。
所以满足$\angle BPC = 90^{\circ}$的点$P$的个数为$2$，答案是C。

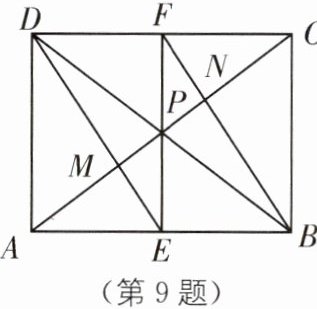
9. 如图,在矩形 $ ABCD $ 中,$ AB = 2 $,$ BC = \sqrt{3} $,$ E,F $ 分别是 $ AB,CD $ 的中点,线段 $ DE,BF,EF $ 分别交对角线 $ AC $ 于点 $ M,N,P $,则以图中的线段为边的直角三角形共有(D)。

A.8 个
B.12 个
C.16 个
D.20 个

答案： D