2025年实验班提优训练暑假衔接版八升九年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版八升九年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
12. 如图,$AC$,$BD相交于点O$,$AC= BD$,$AB= CD$,写出图中两对相等的角____。


∠A=∠D,∠B=∠C
答案:
∠A=∠D,∠B=∠C
13. 如图,在$\triangle ABC$中,$\angle C= 90^{\circ}$,$AD平分\angle BAC$,$AB= 10$,$CD= 4$,则$\triangle ABD$的面积是
20
。
答案:
20
14. 如图,一副含$30^{\circ}和45^{\circ}角的三角板ABC和EDF$拼合在一个平面上,边$AC与EF$重合,$AC= 12cm$。当点$E从点A出发沿AC$方向滑动时,点$F同时从点C出发沿射线BC$方向滑动。当点$E从点A滑动到点C$时,点$D$运动的路径长为____$cm$;连接$BD$,则$\triangle ABD$的面积最大值为____$cm^{2}$。
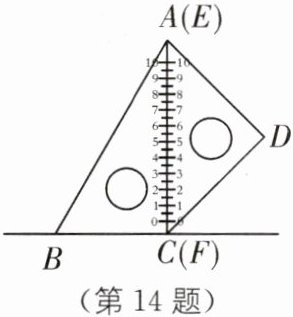

答案:
(24−12$\sqrt{2}$) (24$\sqrt{3}$+36$\sqrt{2}$−12$\sqrt{6}$) [解析]本题考查了轨迹、全等三角形的判定和性质、等腰直角三角形的性质、角平分线的性质、三角形的面积公式等知识.
∵AC=12cm,∠BAC=30°,∠DEF=45°,
∴BC=4$\sqrt{3}$cm,AB=8$\sqrt{3}$cm,ED=DF=6$\sqrt{2}$cm.
如图
(1),当点E沿AC方向下滑时,得△E'D'F',过点D'作D'N⊥AC于点N,作D'M⊥BC于点M.
∴∠MD'N=90°,∠E'D'F'=90°.
∴∠E'D'N=∠F'D'M,∠D'NE'=∠D'MF'=90°,E'D'=D'F'.
∴△D'NE'≌△D'MF'(AAS).
∴D'N=D'M,D'N⊥AC,D'M⊥CM.
∴CD'平分∠ACM,即点E沿AC方向下滑时,点D'在射线CD上移动.
∴当ED'⊥AC时,DD'的值最大,最大值为$\sqrt{2}$ED−CD=(12−6$\sqrt{2}$)cm.
∴当点E从点A滑动到点C时,点D运动的路径长为2×(12−6$\sqrt{2}$)=(24−12$\sqrt{2}$)cm.
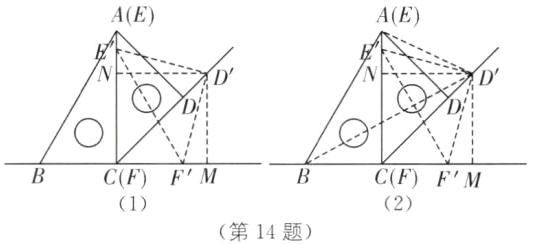
如图
(2),连接BD',AD'.
$∵S_{△AD'B}=S_{△ABC}+S_{△AD'C}-S_{△BD'C},$
$∴S_{△AD'B}$=$\frac{1}{2}$BC·AC+$\frac{1}{2}$AC·D'N−$\frac{1}{2}$BC·D'M=24$\sqrt{3}$+$\frac{1}{2}$(12−4$\sqrt{3}$)D'N.
当E'D'⊥AC时,D'N最大,
∴$S_{△AD'B}$的最大值为24$\sqrt{3}$+$\frac{1}{2}$(12−4$\sqrt{3}$)×6$\sqrt{2}$=(24$\sqrt{3}$+36$\sqrt{2}$−12$\sqrt{6}$)cm².
(24−12$\sqrt{2}$) (24$\sqrt{3}$+36$\sqrt{2}$−12$\sqrt{6}$) [解析]本题考查了轨迹、全等三角形的判定和性质、等腰直角三角形的性质、角平分线的性质、三角形的面积公式等知识.
∵AC=12cm,∠BAC=30°,∠DEF=45°,
∴BC=4$\sqrt{3}$cm,AB=8$\sqrt{3}$cm,ED=DF=6$\sqrt{2}$cm.
如图
(1),当点E沿AC方向下滑时,得△E'D'F',过点D'作D'N⊥AC于点N,作D'M⊥BC于点M.
∴∠MD'N=90°,∠E'D'F'=90°.
∴∠E'D'N=∠F'D'M,∠D'NE'=∠D'MF'=90°,E'D'=D'F'.
∴△D'NE'≌△D'MF'(AAS).
∴D'N=D'M,D'N⊥AC,D'M⊥CM.
∴CD'平分∠ACM,即点E沿AC方向下滑时,点D'在射线CD上移动.
∴当ED'⊥AC时,DD'的值最大,最大值为$\sqrt{2}$ED−CD=(12−6$\sqrt{2}$)cm.
∴当点E从点A滑动到点C时,点D运动的路径长为2×(12−6$\sqrt{2}$)=(24−12$\sqrt{2}$)cm.

如图
(2),连接BD',AD'.
$∵S_{△AD'B}=S_{△ABC}+S_{△AD'C}-S_{△BD'C},$
$∴S_{△AD'B}$=$\frac{1}{2}$BC·AC+$\frac{1}{2}$AC·D'N−$\frac{1}{2}$BC·D'M=24$\sqrt{3}$+$\frac{1}{2}$(12−4$\sqrt{3}$)D'N.
当E'D'⊥AC时,D'N最大,
∴$S_{△AD'B}$的最大值为24$\sqrt{3}$+$\frac{1}{2}$(12−4$\sqrt{3}$)×6$\sqrt{2}$=(24$\sqrt{3}$+36$\sqrt{2}$−12$\sqrt{6}$)cm².
15. 在$\triangle ABC$中,$\angle C= 90^{\circ}$,$BC= 4cm$,$\angle BAC的平分线交BC于点D$,且$BD:DC= 5:3$,则点$D到AB$的距离为____
1.5cm
。
答案:
1.5cm
16. 在$\triangle ABC$中,高$AD和BE交于点H$,且$BH= AC$,则$\angle ABC= $
45°或135°
。
答案:
45°或135°
17. 如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三边所对的角的关系是
相等或互补
。
答案:
相等或互补
18. 在数学活动课上,小明提出这样一个问题:$\angle B= \angle C= 90^{\circ}$,$E是BC$的中点,$DE平分\angle ADC$,$\angle CED= 35^{\circ}$,如图,则$\angle EAB$是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是
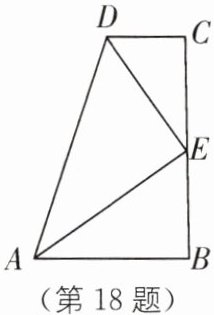
35°
。
答案:
35°
19. 如图,点$D$,$E分别在AB$,$AC$上,$DE// BC$,$F是AD$上一点,$FE的延长线交BC的延长线于点G$。求证:
(1)$\angle EGH>\angle ADE$;
(2)$\angle EGH= \angle ADE+\angle A+\angle AEF$。

(1)$\angle EGH>\angle ADE$;
(2)$\angle EGH= \angle ADE+\angle A+\angle AEF$。

答案:
(1)
∵∠EGH是△FBG的外角,
∴∠EGH>∠B.又DE//BC,
∴∠B=∠ADE.
∴∠EGH>∠ADE.
(2)
∵∠BFE是△AFE的外角,
∴∠BFE=∠A+∠AEF.
∵∠EGH是△BFG的外角,
∴∠EGH=∠B+∠BFE.
∴∠EGH=∠B+∠A+∠AEF.
又DE//BC,
∴∠B=∠ADE.
∴∠EGH=∠ADE+∠A+∠AEF.
(1)
∵∠EGH是△FBG的外角,
∴∠EGH>∠B.又DE//BC,
∴∠B=∠ADE.
∴∠EGH>∠ADE.
(2)
∵∠BFE是△AFE的外角,
∴∠BFE=∠A+∠AEF.
∵∠EGH是△BFG的外角,
∴∠EGH=∠B+∠BFE.
∴∠EGH=∠B+∠A+∠AEF.
又DE//BC,
∴∠B=∠ADE.
∴∠EGH=∠ADE+∠A+∠AEF.
20. (1)如图,在三角形纸片$ABC$中,$\angle A= 64^{\circ}$,$\angle B= 76^{\circ}$,将纸片的一角折叠,使点$C落在\triangle ABC$内部,折痕为$MN$。如果$\angle 1= 17^{\circ}$,求$\angle 2$的度数。
(2)小明在(1)的解题过程中发现$\angle 1+\angle 2= 2\angle C$,小明的这个发现对任意的三角形都成立吗?请说明理由。
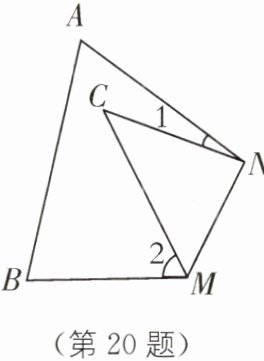
(2)小明在(1)的解题过程中发现$\angle 1+\angle 2= 2\angle C$,小明的这个发现对任意的三角形都成立吗?请说明理由。

答案:
(1)
∵∠A=64°,∠B=76°,
∴∠C=180°−∠A−∠B=180°−64°−76°=40°.
∵∠1=17°,
∴∠CNM=$\frac{180° - ∠1}{2}$=81.5°.
∴在△CMN中,∠CMN=180°−∠C−∠CNM=180°−40°−81.5°=58.5°.
∴∠2=180°−2∠CMN=180°−2×58.5°=63°.
(2)小明的这个发现对任意的三角形都成立.理由如下:
由题意,得2∠CNM+∠1=180°,2∠CMN+∠2=180°.
∴2(∠CNM+∠CMN)+∠1+∠2=360°.
∵∠C+∠CNM+∠CMN=180°,
∴∠CNM+∠CMN=180°−∠C.
∴2(180°−∠C)=360°−(∠1+∠2).
∴∠1+∠2=2∠C.
(1)
∵∠A=64°,∠B=76°,
∴∠C=180°−∠A−∠B=180°−64°−76°=40°.
∵∠1=17°,
∴∠CNM=$\frac{180° - ∠1}{2}$=81.5°.
∴在△CMN中,∠CMN=180°−∠C−∠CNM=180°−40°−81.5°=58.5°.
∴∠2=180°−2∠CMN=180°−2×58.5°=63°.
(2)小明的这个发现对任意的三角形都成立.理由如下:
由题意,得2∠CNM+∠1=180°,2∠CMN+∠2=180°.
∴2(∠CNM+∠CMN)+∠1+∠2=360°.
∵∠C+∠CNM+∠CMN=180°,
∴∠CNM+∠CMN=180°−∠C.
∴2(180°−∠C)=360°−(∠1+∠2).
∴∠1+∠2=2∠C.
查看更多完整答案,请扫码查看


