《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

1.(张家界中考)下列图形中,既是轴对称图形又是中心对称图形的为( )

答案： D

2. 下列四个图案中,既可用旋转来分析整个图案的形成过程,又可用平移来分析整个图案的形成过程的是( )

答案： C

3.(南充中考)如图,将直角三角尺ABC绕顶点A按顺时针方向旋转到△AB'C',点B'恰好落在CA的延长线上,∠B= 30°,∠C= 90°,则∠BAC'的度数为( )

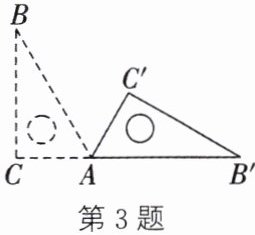
A.90°
B.60°
C.45°
D.30°

答案： B

4. 某数学兴趣小组开展动手操作活动,设计了如图所示的三个图形.现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )

A.甲图形所用的铁丝最长
B.乙图形所用的铁丝最长
C.丙图形所用的铁丝最长
D.三个图形所用的铁丝一样长

答案： D

5.(湖州中考)如图,将△ABC沿BC方向平移1cm得到对应的△A'B'C'.若B'C= 2cm,则BC'的长是( )

A.2cm
B.3cm
C.4cm
D.5cm

答案： C

6. 如图,在方格纸中,△ABC经过变换得到△DEF,下列对变换过程叙述正确的是( )

A.把△ABC向左平移8格,再按逆时针方向旋转90°
B.把△ABC绕点C按逆时针方向旋转90°,再向左平移8格
C.把△ABC向左平移8格,再按顺时针方向旋转90°
D.把△ABC绕点C按顺时针方向旋转90°,再向左平移8格

答案： D

7.(天津中考)如图,在△ABC中,AB= AC.若M是边BC上任意一点,将△ABM绕点A按逆时针方向旋转得到△ACN,点M的对应点为N,连接MN,则下列结论一定正确的是( )

A.AB= AN
B.AB//NC
C.∠AMN= ∠ACN
D.MN⊥AC

答案： C

8.(包头中考)如图,在Rt△ABC中,∠ACB= 90°,∠A= 30°,BC= 2,将△ABC绕点C按顺时针方向旋转得到△A'B'C,其中点A'与点A对应,点B'与点B对应.若点B'恰好落在边AB上,则点A到直线A'C的距离为( )

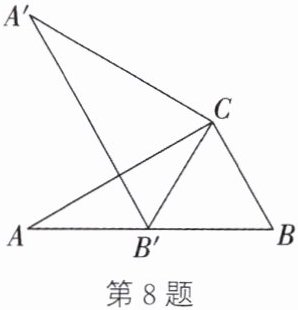
A.3√3
B.2√3
C.3
D.2
答案讲解

答案：
C　解析:如图，连接AA',
∵∠ACB=90°,∠BAC=30°,BC=2,
∴易得AC=2$\sqrt{3}$,∠B=60°.
∵将△ABC 绕点C按顺时针方向旋转得到△A'B'C,
∴CA=CA',CB=CB',∠ACA'=∠BCB'.
∵CB=CB',∠B=60°,
∴△CBB'为等边三角形.
∴　∠BCB'=60°.
∴∠ACA'=60°.
∴△CAA'为等边三角形.过点A作AD⊥A'C于点D.
∴易得CD=$\frac{1}{2}$AC=$\sqrt{3}$.
∴由勾股定理,易得AD=3.
∴点A到直线A'C的距离为3.