《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

1. 矩形的定义：
有一个角是______的______四边形叫做矩形.
2. 矩形的性质：
(1) 矩形的四个角都是______.
(2) 矩形的对角线______.
3. 直角三角形斜边上的中线的性质：直角三角形斜边上的中线等于斜边的______.
4. 矩形的判定：
(1) 对角线______的______是矩形.
(2) 有三个角是______角的______是矩形.

答案： 1. 直角 平行 2.（1）直角 （2）相等 3. 一半 4.（1）相等 平行四边形 （2）直 四边形

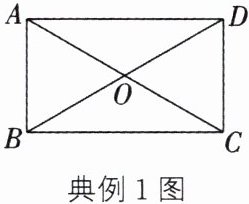
典例1 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB= 60°,AC= 6cm,则AB的长是( )


A.3cm
B.6cm
C.10cm
D.12cm
点拨 根据矩形的对角线相等且互相平分可得OA= OB,由∠AOB= 60°,判断出△AOB是等边三角形,根据等边三角形的性质求出AB的长即可.
解答：
解有所悟：矩形的每条对角线将矩形分成两个全等的直角三角形,两条对角线将矩形分成四个等腰三角形. 特别地,在对角线所夹锐角为60°的矩形中,两条对角线将矩形分成四个三角形,其中矩形的宽所在的三角形是等边三角形；每条对角线将矩形分成两个含有30°角的直角三角形. 因此解决矩形问题常用到直角三角形和等腰(边)三角形的性质.

答案： A 解析：
∵ 四边形 ABCD 是矩形，
∴ OA=$\frac{1}{2}$AC，OB=$\frac{1}{2}$BD，AC=BD=6 cm.
∴ OA=OB=3 cm.
∵ ∠AOB=60°，
∴ △AOB 是等边三角形.
∴ AB=OA=3 cm.

典例2 (宜昌中考)如图,在矩形ABCD中,E是边AD上一点,F,G分别是BE,CE的中点,连接AF,DG,FG. 若AF= 3,DG= 4,FG= 5,则矩形ABCD的面积为______.

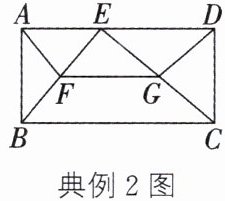
点拨 由矩形的性质得出∠BAE= ∠CDE= 90°,AD//BC,由直角三角形斜边上的中线的性质及三角形中位线定理求出BE,CE,BC的长,由勾股定理的逆定理得出△BCE是直角三角形,再计算$S_{△BCE}= \frac {1}{2}BE·CE,$从而求出矩形ABCD的面积.
解答：
解有所悟：与中点有关的知识有直角三角形斜边上的中线的性质、三角形中位线定理、等腰三角形三线合一的性质等,有时会综合几种知识于同一题中,要注意灵活运用. 必要时可添加辅助线,构造相关性质的基本图形求解.

答案： 48 解析：
∵ 四边形 ABCD 是矩形，
∴ ∠BAE=∠CDE=90°，AD//BC.
∵ F，G 分别是 BE，CE 的中点，AF=3，DG=4，FG=5，
∴ BE=2AF=6，CE=2DG=8，BC=2FG=10.
∴ BE²+CE²=BC².
∴ △BCE 是直角三角形，且∠BEC=90°.
∴ S_{△BCE}=$\frac{1}{2}$BE·CE=$\frac{1}{2}$×6×8=24.
∵ AD//BC，
∴ S_{矩形ABCD}=2S_{△BCE}=2×24=48.