第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 菱形的定义:
有一组邻边______的______四边形叫做菱形.
2. 菱形的性质:
(1) 菱形的四条边______.
(2) 菱形的对角线互相______.
3. 菱形的判定:
(1) 对角线______的______是菱形.
(2) 四边______的______是菱形.
有一组邻边______的______四边形叫做菱形.
2. 菱形的性质:
(1) 菱形的四条边______.
(2) 菱形的对角线互相______.
3. 菱形的判定:
(1) 对角线______的______是菱形.
(2) 四边______的______是菱形.
答案:
1. 相等 平行 2.(1)相等 (2)垂直 3.(1)互相垂直 平行四边形 (2)相等 四边形
典例1 (达州中考)如图,菱形ABCD的对角线AC,BD相交于点O,AC= 24,BD= 10,则菱形ABCD的周长为______.
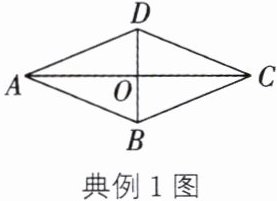
点拨 由菱形的对角线互相垂直且平分,在直角三角形中利用勾股定理求出菱形的边长,再根据菱形的四条边相等求出周长.
解答:
解有所悟:解决此类问题的关键是熟记菱形的性质,由对角线互相垂直平分得直角三角形,在直角三角形中,运用勾股定理求出菱形的边长.

点拨 由菱形的对角线互相垂直且平分,在直角三角形中利用勾股定理求出菱形的边长,再根据菱形的四条边相等求出周长.
解答:
解有所悟:解决此类问题的关键是熟记菱形的性质,由对角线互相垂直平分得直角三角形,在直角三角形中,运用勾股定理求出菱形的边长.
答案:
52 解析:
∵ 四边形ABCD是菱形,
∴ AB=BC=CD=DA,AC⊥BD,AO=CO,BO=DO.
∵ AC=24,BD=10,
∴ AO=$\frac{1}{2}$AC=12,BO=$\frac{1}{2}$BD=5.在Rt△AOB中,AB=$\sqrt{AO^2+BO^2}$=$\sqrt{12^2+5^2}$=13,
∴ 菱形ABCD的周长为13×4=52.
∵ 四边形ABCD是菱形,
∴ AB=BC=CD=DA,AC⊥BD,AO=CO,BO=DO.
∵ AC=24,BD=10,
∴ AO=$\frac{1}{2}$AC=12,BO=$\frac{1}{2}$BD=5.在Rt△AOB中,AB=$\sqrt{AO^2+BO^2}$=$\sqrt{12^2+5^2}$=13,
∴ 菱形ABCD的周长为13×4=52.
典例2 (嘉兴中考)小惠自编一道题目:如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB= OD. 求证:四边形ABCD是菱形. 她将自己的证明过程与同学小洁进行交流.
小惠:证明:∵AC⊥BD,OB= OD,∴AC垂直平分BD. ∴AB= AD,CB= CD. ∴四边形ABCD是菱形.
小洁说:“这道题目还缺少条件,需要补充一个条件才能证明.”
若赞同小惠的证法,请在方框内打“√”;若赞同小洁的说法,请你补充一个条件,并证明.
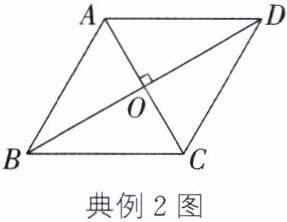
点拨 根据“对角线互相垂直的平行四边形是菱形”进行分析推理.
解答:
解有所悟:解决此类问题的关键是熟记菱形的判定方法,结合题意选择合适的方法进行判断及证明.
小惠:证明:∵AC⊥BD,OB= OD,∴AC垂直平分BD. ∴AB= AD,CB= CD. ∴四边形ABCD是菱形.
小洁说:“这道题目还缺少条件,需要补充一个条件才能证明.”
若赞同小惠的证法,请在方框内打“√”;若赞同小洁的说法,请你补充一个条件,并证明.

点拨 根据“对角线互相垂直的平行四边形是菱形”进行分析推理.
解答:
解有所悟:解决此类问题的关键是熟记菱形的判定方法,结合题意选择合适的方法进行判断及证明.
答案:
赞同小洁的说法.补充的条件不唯一,如OA=OC.
∵ OA=OC,OB=OD,
∴ 四边形ABCD是平行四边形.又
∵ AC⊥BD,
∴ 四边形ABCD是菱形.
∵ OA=OC,OB=OD,
∴ 四边形ABCD是平行四边形.又
∵ AC⊥BD,
∴ 四边形ABCD是菱形.
查看更多完整答案,请扫码查看


