《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

8. 在平面直角坐标系中,用大小完全相同的长方形纸片摆成如图所示的图案.若点A的坐标是$(-2,5)$,则点B的坐标是( )

A.$(-\frac {14}{3},\frac {11}{3})$
B.$(-\frac {20}{3},\frac {14}{3})$
C.$(-6,5)$
D.$(-6,4)$

答案： D

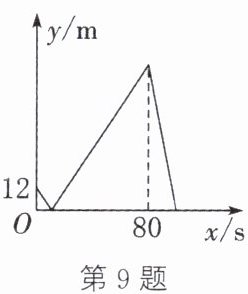
9. (赤峰中考)甲、乙两人在一条长400m的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3s,在跑步过程中,甲、乙两人间的距离$y(m)与乙出发的时间x(s)$之间的函数关系如图所示.有下列结论：①乙的速度为5m/s；②离开起点后,甲、乙两人第一次相遇时,距离起点12m；③甲、乙两人之间的距离超过32m时,x的取值范围是$44\lt x＜89$；④乙到达终点时,甲距离终点还有68m.其中,正确的有( )

A.4个
B.3个
C.2个
D.1个

答案： B　解析:由函数图象,得甲的速度为12÷3 = 4(m/s),乙的速度为400÷80 = 5(m/s).故①正确.根据题意,得5x = 12 + 4x,解得x = 12.
∴离开起点后，甲、乙两人第一次相遇时,距离起点12×5 = 60(m).故②错误.当甲、乙两人之间的距离超过32m时，{(5 - 4)x - 12 ＞ 32, 4(x + 3) ＜ 400 - 32}可得44 ＜ x ＜ 89.故③正确.
∵乙到达终点时，所用时间为80s,甲先出发3s,
∴此时甲跑步的时间为83s.
∴甲跑步的路程为83×4 = 332(m).
∴乙到达终点时，甲距离终点还有400 - 332 = 68(m).故④正确.综上所述，正确的有3个.

10. 如图,在$Rt\triangle ABC$中,$∠C= 90^{\circ },AC= 12,BC= 5$.将$\triangle ABC$绕AB上的点O按顺时针方向旋转$90^{\circ }$,得到$\triangle A'B'C'$,连接$BC'$.若$BC'// A'B'$,则OB的长为( )

A.$\frac {60}{13}$
B.5
C.$\frac {65}{12}$
D.$\frac {24}{5}$

答案： A　解析:如图，连接OC,OC',过点C作CH⊥AB于点H.在Rt△ABC中,
∵∠ACB = 90°,AC = 12,BC = 5,
∴AB = √(5² + 12²) = 13.
∵S△ABC = 1/2AB·CH = 1/2AC·BC,
∴CH = (AC·BC)/AB = (12×5)/13 = 60/13.
∵将△ABC绕AB上的点O按顺时针方向旋转90°,得到△A'B'C',
∴OC = OC',∠COC' = ∠BOB' = 90°.
∵BC'//A'B',
∴∠OBC' = 90°.
∵CH⊥AB,
∴∠CHO = 90° = ∠OBC'.
∵∠COH + ∠C'OB = 90°,∠COH + ∠OCH = 90°,
∴∠OCH = ∠C'OB.在△CHO和△OBC'中,{∠OCH = ∠C'OB,∠CHO = ∠OBC',OC = C'O,}
∴△CHO≌△OBC'.
∴CH = OB = 60/13.

11. 已知$\triangle ABC$的三边长分别是a,b,c,且满足$a^{2}+b^{2}+c^{2}= ab+bc+ac$,则此三角形为______三角形(按边分).

答案： 等边

12. 如图所示为城市某区域的示意图,建立平面直角坐标系后,学校和体育场的坐标分别是$(3,1),(4,-2)$,图中各地点中,离原点最远的是______,距离为______.

答案： 体育场　2√5

13. (长沙中考)如图,在$\triangle ABC$中,按以下步骤作图：①分别以点A,B为圆心,大于$\frac {1}{2}AB$的长为半径画弧,两弧交于P,Q两点；②作直线PQ交AB于点D；③以点D为圆心,AD长为半径画弧,交PQ于点M,连接AM,BM.若$AB= 2\sqrt {2}$,则AM的长为______.

答案： 2

14. (齐齐哈尔中考)若关于x的分式方程$\frac {1}{x-2}+\frac {2}{x+2}= \frac {x+2m}{x^{2}-4}$的解大于1,则m的取值范围是______.

答案： m＞0且m≠1

15. 如图,分别以$Rt\triangle ABC$的斜边AB、直角边AC为边向$\triangle ABC$外作等边三角形ABD和等边三角形ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,连接DF,$∠ACB= 90^{\circ },∠BAC= 30^{\circ }$.有下列结论：①$EF⊥AC$；②四边形ADFE是平行四边形；③$AD= 4AG$；④$FH= \frac {1}{4}BD$.其中,正确的为______(填序号).

答案： ①②③④