《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

10.(丽水中考)如图,在$\triangle ABC$中,$D$,$E$,$F分别是BC$,$AC$,$AB$的中点.若$AB = 6$,$BC = 8$,则四边形$BDEF$的周长是______.

答案： 14

11. 如图,$AD是\triangle ABC$的中线,$CF$,$BE分别垂直于AD$,垂足分别为$F$,$E$,则四边形$BECF$是______,理由是______.

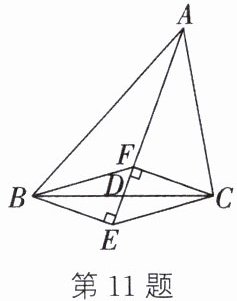
答案： 平行四边形　一组对边平行且相等的四边形是平行四边形

12. 在$□ ABCD$中,$AD = BD$,$BE是边AD$上的高,$\angle EBD = 20^{\circ}$,则$\angle C$的度数为______.

答案：
55°或35°　解析:由题意，可知在等腰三角形ADB中，顶角∠ADB可能是锐角，也可能是钝角，因此需分两种情况讨论.如图①，当∠ADB为锐角时，点E在线段AD上.
∵BE是边AD上的高，
∴∠BED = 90°.又
∵∠EBD = 20°,
∴∠EDB = 70°.
∵AD = BD,
∴∠A = $\frac{1}{2}$×(180° - 70°) = 55°.
∵四边形ABCD是平行四边形，
∴∠C = ∠A = 55°.如图②,当∠ADB为钝角时，点E在线段AD的延长线上.
∵BE是边AD上的高，
∴∠BED = 90°.
∵∠EBD = 20°,
∴∠EDB = 70°.
∴∠ADB = 180° - ∠EDB = 110°.
∵AD = BD,
∴∠A = $\frac{1}{2}$×(180° - 110°) = 35°.
∵四边形ABCD是平行四边形,
∴∠C = ∠A = 35°.综上所述,∠C的度数为55°或35°.易错提示：当平行四边形内出现等腰三角形时因忽略分类讨论而致错。平行四边形被每条对角线分成两个三角形，当平行四边形的一边和一条对角线相等时，分成的两个三角形就是等腰三角形，这时往往容易忽略分类讨论而导致错误。注意：当等腰三角形的角、边、顶点、高等不确定时，要分类讨论。

13. 如图,在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,$AB = 4$,$BC＞AB$,点$D在BC$上,以$AC为对角线的所有平行四边形ADCE$中,$DE$长的最小值是______.

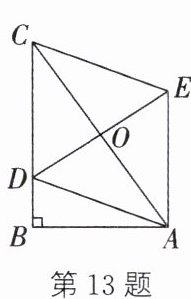
答案： 4

14. 转换法 如图,$\angle A+\angle B+\angle C+\angle D+\angle E+\angle F+\angle G+\angle H= $______.

答案： 720°

15.(临沂中考)如图,在正六边形$ABCDEF$中,$M$,$N是对角线BE$上的两点.添加下列条件中的一个：①$BM = EN$；②$\angle FAN = \angle CDM$；③$AM = DN$；④$\angle AMB = \angle DNE$.其中,能使四边形$AMDN$是平行四边形的为______(填序号).

答案： ①②④

16. 如图,$AD$,$BE分别是\triangle ABC$的中线和角平分线,$AD\perp BE$,$AE= \frac{1}{3}AC$,$AD = BE = 6$,则$AC$的长为______.

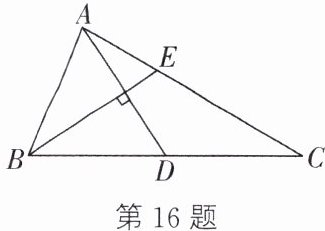
答案：
$\frac{9\sqrt{5}}{2}$　解析:如图,设AD,BE交于点O,取EC的中点F,连接DF.由题意，知D是BC的中点，
∴DF是△BEC的中位线.
∴DF = $\frac{1}{2}$BE,DF//BE.
∵BE是△ABC的角平分线,
∴∠ABO = ∠DBO.
∵AD⊥BE,
∴∠AOB = ∠DOB = 90°.在△ABO和△DBO中，$\begin{cases}∠ABO = ∠DBO \\ BO = BO \\ ∠AOB = ∠DOB\end{cases}$，
∴△ABO≌△DBO.
∴AO = DO = $\frac{1}{2}$AD = 3.
∵AE = $\frac{1}{3}$AC,F是EC的中点,
∴AE = EF.
∴OE是△ADF的中位线,
∴OE = $\frac{1}{2}$DF = $\frac{1}{4}$BE = $\frac{1}{4}$×6 = $\frac{3}{2}$.
∵在Rt△AOE中,由勾股定理,得AE = $\sqrt{AO^{2}+OE^{2}}$ = $\sqrt{3^{2}+(\frac{3}{2})^{2}}$ = $\frac{3\sqrt{5}}{2}$,
∴AC = 3AE = $\frac{9\sqrt{5}}{2}$.方法点金：巧构三角形中位线解题。三角形的中位线定理具有证明位置关系和数量关系两方面的作用，在几何证明题中有着重要的应用。若图形中存在中点，则可以构造三角形及三角形的中位线，从而利用三角形的中位线定理证明。

17.(6分)如图,小东在足球场的中间位置,从点$A$出发,每走$6m向左转60^{\circ}$.
(1)小东能否走回点$A$？若能回到点$A$,则需走多少米？走过的路径是一个什么图形(路径为点$A\to点B\to点C…\to$)？
(2)求这个图形的内角和.

答案：
(1)小东能走回点A.回到点A需走360÷60×6 = 36(m).走过的路径是一个边长为6m的正六边形.
(2)正六边形的内角和为(6 - 2)×180° = 720°.

18.(6分)(宿迁中考)如图,在$□ ABCD$中,$E$,$F分别是边AB$,$CD$的中点. 求证：$AF = CE$.

答案：
∵四边形ABCD是平行四边形，
∴AB//CD,AB = CD.
∵E,F分别是边AB,CD的中点，
∴AE = BE = CF = DF.
∴四边形AECF是平行四边形.
∴AF = CE.