第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
5.(恩施中考)九年级(1)班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛,在相同的条件下,分别对两名男生进行了八次一分钟跳绳测试。现将测试结果绘制成如下不完整的统计表和如图所示的统计图,请根据统计图表中的信息解答下列问题:
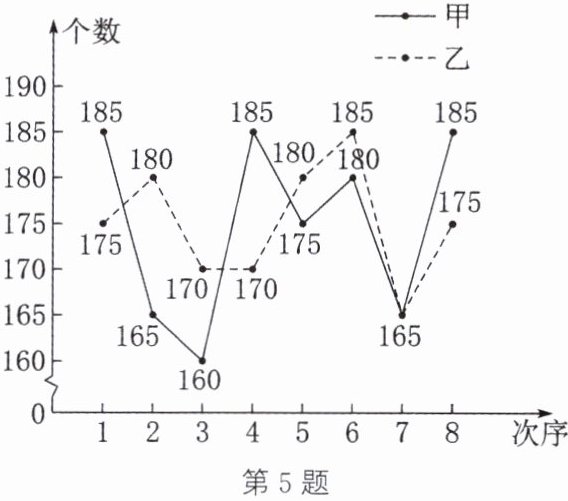
(1)求$a$,$b$的值。
(2)若九年级(1)班选一名成绩稳定的选手参赛,你认为应选谁?请说明理由。
(3)根据以上的数据分析,请你运用所学的统计知识,任选两个角度评价甲、乙两名男生一分钟跳绳成绩谁优。
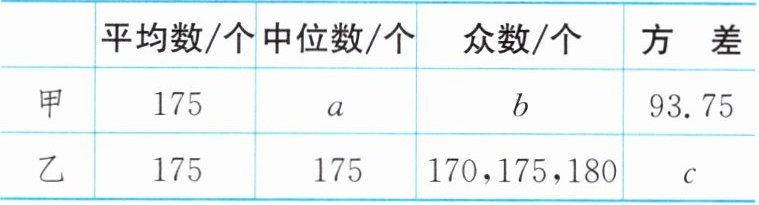
| |平均数/个|中位数/个|众数/个|方差|
|甲|175|$a$|$b$|93.75|
|乙|175|175|170,175,180|$c$|

(1)求$a$,$b$的值。
(2)若九年级(1)班选一名成绩稳定的选手参赛,你认为应选谁?请说明理由。
(3)根据以上的数据分析,请你运用所学的统计知识,任选两个角度评价甲、乙两名男生一分钟跳绳成绩谁优。
| |平均数/个|中位数/个|众数/个|方差|
|甲|175|$a$|$b$|93.75|
|乙|175|175|170,175,180|$c$|

答案:
(1)$a=177.5$;$b=185$.(2)应选乙.理由:乙的方差为$\frac{1}{8}×[2×(175 - 175)^{2}+2×(180 - 175)^{2}+2×(170 - 175)^{2}+(185 - 175)^{2}+(165 - 175)^{2}]=37.5$.
∵ 乙的方差小于甲的方差,
∴ 乙的成绩比甲的成绩稳定.
∴ 应选乙.(3)角度选择不唯一,如从平均数和中位数相结合看,甲的一分钟跳绳成绩优.
∵ 乙的方差小于甲的方差,
∴ 乙的成绩比甲的成绩稳定.
∴ 应选乙.(3)角度选择不唯一,如从平均数和中位数相结合看,甲的一分钟跳绳成绩优.
6.(嘉兴中考)在推进嘉兴市城乡生活垃圾分类的行动中,某社区为了了解居民掌握垃圾分类知识的情况进行了测试。其中A,B两小区分别有500名居民参加了测试,社区从中各随机抽取50名居民的成绩进行整理得到部分信息:
【信息一】A小区50名居民成绩的频数直方图如图所示(每一组含前一个边界值,不含后一个边界值):

【信息二】在信息一的图中,从左往右第四组的成绩如下表(单位:分):
|75|75|79|79|79|79|80|80|81|82|82|83|83|84|84|84|

【信息三】A,B两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差如下表(部分空缺):
|小区|平均数/分|中位数/分|众数/分|优秀率|方差|
|A|75.1|?|79|40%|277|
|B|75.1|77|76|45%|211|

根据以上信息,回答下列问题:
(1)求A小区50名居民成绩的中位数;
(2)请估计A小区500名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,选择合适的统计量分析A,B两小区参加测试的居民掌握垃圾分类知识的情况。
【信息一】A小区50名居民成绩的频数直方图如图所示(每一组含前一个边界值,不含后一个边界值):

【信息二】在信息一的图中,从左往右第四组的成绩如下表(单位:分):
|75|75|79|79|79|79|80|80|81|82|82|83|83|84|84|84|

【信息三】A,B两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差如下表(部分空缺):
|小区|平均数/分|中位数/分|众数/分|优秀率|方差|
|A|75.1|?|79|40%|277|
|B|75.1|77|76|45%|211|

根据以上信息,回答下列问题:
(1)求A小区50名居民成绩的中位数;
(2)请估计A小区500名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,选择合适的统计量分析A,B两小区参加测试的居民掌握垃圾分类知识的情况。
答案:
(1)
∵ 有 50 名居民,$4 + 8 + 12=24$(名),
∴ 中位数落在第四组,中位数为 75 分.(2)$500×\frac{16 + 10 - 2}{50}=240$(名).
∴ 估计 A 小区 500 名居民成绩能超过平均数的人数为 240.(3)从平均数看,A,B 两小区居民对垃圾分类知识掌握情况的平均水平相同;从中位数看,B 小区至少有一半的居民成绩高于平均数;从众数看,A 小区得79 分的人数最多,B 小区得 76 分的人数最多;从优秀率看,B 小区的优秀人数多于 A 小区;从方差看,B 小区居民对垃圾分类知识掌握的情况比 A 小区稳定.
∵ 有 50 名居民,$4 + 8 + 12=24$(名),
∴ 中位数落在第四组,中位数为 75 分.(2)$500×\frac{16 + 10 - 2}{50}=240$(名).
∴ 估计 A 小区 500 名居民成绩能超过平均数的人数为 240.(3)从平均数看,A,B 两小区居民对垃圾分类知识掌握情况的平均水平相同;从中位数看,B 小区至少有一半的居民成绩高于平均数;从众数看,A 小区得79 分的人数最多,B 小区得 76 分的人数最多;从优秀率看,B 小区的优秀人数多于 A 小区;从方差看,B 小区居民对垃圾分类知识掌握的情况比 A 小区稳定.
查看更多完整答案,请扫码查看


