《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

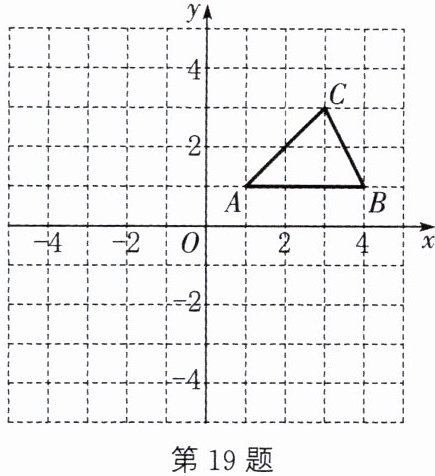
19.(5 分)如图,在平面直角坐标系中,$\triangle ABC$ 的顶点坐标分别是 $A(1, 1)$,$B(4, 1)$,$C(3, 3)$.
(1)将 $\triangle ABC$ 向下平移 5 个单位长度得到 $\triangle A_{1}B_{1}C_{1}$,请画出 $\triangle A_{1}B_{1}C_{1}$；
(2)将 $\triangle ABC$ 绕原点 $O$ 按逆时针方向旋转 $90^{\circ}$ 后得到 $\triangle A_{2}B_{2}C_{2}$,请画出 $\triangle A_{2}B_{2}C_{2}$；
(3)判断以 $O$,$A_{1}$,$B$ 为顶点的三角形的形状(不需要说明理由).

答案：

(1)如图,△A₁B₁C₁即为所求.
(2)如图,△A₂B₂C₂即为所求.
(3)以 O,A₁,B 为顶点的三角形为等腰直角三角形.
　　　　　

20.(5 分)(张家界中考)先化简 $(1 - \frac{1}{a - 1}) ÷ \frac{a - 2}{2} + \frac{a - 1}{a^{2} - 2a + 1}$,再从 $1$,$2$,$3$ 中选一个适当的数作为 $a$ 的值代入求值.

答案： 原式=(a - 2)/(a - 1)·2/(a - 2)+(a - 1)/(a² - 2a + 1)=2/(a - 1)+1/(a - 1)=3/(a - 1).
∵a = 1,2时分式无意义,
∴a = 3.当a = 3时,原式=3/2.

21.(8 分)(聊城中考)为了解决雨季时城市内涝的难题,某市决定对部分老街道的地下管网进行改造. 在改造一段长 3600 米的街道地下管网时,每天的施工效率比原计划提高了 $20\%$,按这样的进度可以比原计划提前 10 天完成任务.
(1)求实际施工时,每天改造地下管网的长度；
(2)施工进行 20 天后,为了减少对交通的影响,施工单位决定再次加快施工进度,以确保总工期不超过 40 天,那么以后每天改造地下管网至少还要增加多少米？

答案：
(1)设原计划每天改造地下管网 x 米,则实际施工时,每天改造地下管网(1 + 20%)x 米.由题意,得3600/x - 3600/((1 + 20%)x)=10,解得x = 60.经检验,x = 60是原方程的解,且符合题意.60×(1 + 20%)=72(米).
∴实际施工时,每天改造地下管网的长度是72米.
(2)设以后每天改造地下管网还要增加 m 米.由题意,得(40 - 20)×(72 + m)≥3600 - 72×20,解得m≥36.
∴以后每天改造地下管网至少还要增加36米.