《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

1.(烟台中考)一个正多边形每个内角与它相邻外角的度数比为3:1,则这个正多边形是( )

A.正方形
B.正六边形
C.正八边形
D.正十边形

答案： C

2.(安顺中考)如图,在$□ ABCD$中,$\angle ABC的平分线交AD于点E$,$\angle BCD的平分线交AD于点F$.若$AB = 3$,$AD = 4$,则$EF$的长是( )

A.1
B.2
C.2.5
D.3

答案： B

3. 一个多边形的内角和比其外角和的2倍多$180^{\circ}$,则该多边形的对角线的条数是( )

A.12
B.13
C.14
D.15

答案： C

4.(河北中考)依据所标数据,下列一定为平行四边形的是( )


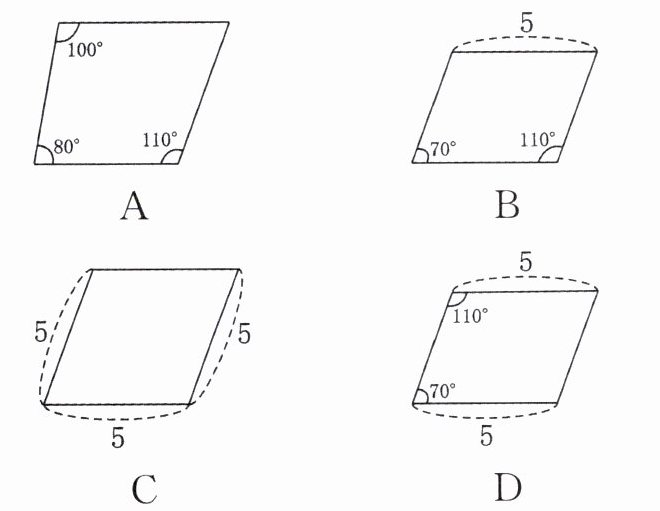
A.
B.
C.
D.

答案： D

5.(益阳中考)如图,在$□ ABCD$中,$AB = 8$,$E是AB$上一点,$AE = 3$,连接$DE$,过点$C作CF// DE$,交$AB的延长线于点F$,则$BF$的长为( )

A.5
B.4
C.3
D.2

答案： C

6.(大庆中考)如图,将$□ ABCD沿对角线BD$折叠,使点$A落在点E$处.若$\angle 1 = 56^{\circ}$,$\angle 2 = 42^{\circ}$,则$\angle A$的度数为( )

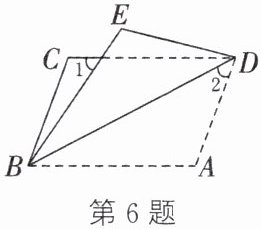
A.$108^{\circ}$
B.$109^{\circ}$
C.$110^{\circ}$
D.$111^{\circ}$

答案： C

7. 如图,在$\triangle ABC$中,$M是BC$的中点,$AN平分\angle BAC$,$BN\perp AN于点N$.若$AB = 7$,$MN = 3$,则$AC$的长为( )

A.14
B.12
C.13
D.11

答案：
C　解析:如图,延长BN交AC于点D.
∵BN⊥AN,
∴∠ANB = ∠AND = 90°.
∵AN平分∠BAC,
∴∠NAB = ∠NAD.在△ANB和△AND中，$\begin{cases}∠NAB = ∠NAD \\ AN = AN \\ ∠ANB = ∠AND = 90°\end{cases}$，
∴△ANB≌△AND.
∴AB = AD = 7,BN = DN.
∵M是BC的中点，
∴MN为△BCD的中位线，
∴DC = 2MN = 6.
∴AC = AD + CD = 13.

8. 如图,在$□ ABCD$中,$\angle ABD = 30^{\circ}$,$AB = 4$,$AE\perp BD于点E$,$CF\perp BD于点F$,且$E$,$F恰好是BD$的三等分点,延长$AE$,$CF分别交CD$,$AB于点N$,$M$,连接$EM$,$FN$.若$M$,$N分别是AB$,$CD$的中点,则四边形$MENF$的面积是( )

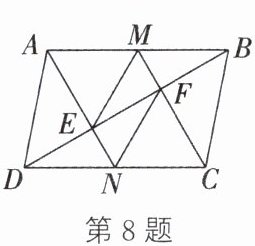
A.$3\sqrt{3}$
B.$\sqrt{3}$
C.$3\sqrt{2}$
D.$\sqrt{2}$

答案： B　解析:
∵AB = 4,M是AB的中点,
∴BM = 2.又
∵CF⊥BD,∠ABD = 30°,
∴在Rt△BFM中,易得MF = 1,BF = $\sqrt{3}$.
∵四边形ABCD是平行四边形，
∴AB//CD.
∴∠BDC = ∠ABD = 30°,同理在Rt△DEN中,可得EN = 1,
∴EN = MF.
∵AE⊥BD,CF⊥BD,
∴MF//EN.
∴四边形MENF是平行四边形.
∵E,F恰好是BD的三等分点，
∴EF = BF = $\sqrt{3}$,
∴四边形MENF的面积 = 1×$\sqrt{3}$ = $\sqrt{3}$.

9.(广州中考)如图,在$□ ABCD$中,$AD = 10$,对角线$AC与BD相交于点O$,$AC + BD = 22$,则$\triangle BOC$的周长为______.

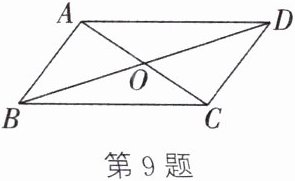
答案： 21