《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

23. (8分)(绍兴中考)如图,在$\triangle ABC$中,$\angle A = 40^{\circ}$,点$D$,$E分别在边AB$,$AC$上,$BD = BC = CE$,连接$CD$,$BE$.
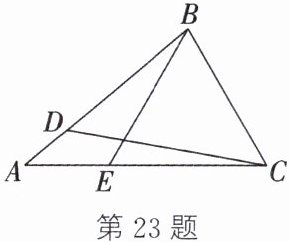
(1)若$\angle ABC = 80^{\circ}$,求$\angle BDC$,$\angle ABE$的度数;
(2)判断$\angle BEC与\angle BDC$之间的数量关系,并说明理由.

答案：
(1)
∵∠ABC=80°,BD=BC,
∴∠BDC=∠BCD=1/2×(180° - 80°)=50°.
∵∠A=40°,∠ABC=80°,
∴∠ACB=180° - 40° - 80°=60°.
∵CE=BC,
∴△BCE是等边三角形.
∴∠EBC=60°.
∴∠ABE=∠ABC - ∠EBC=80° - 60°=20°.
(2)∠BEC+∠BDC=110°.理由:设∠BEC=α,∠BDC=β.
∵CE=BC,
∴∠CBE=∠BEC=α.又
∵α=∠A+∠ABE=40°+∠ABE,
∴∠ABC=∠ABE+∠CBE=∠A+2∠ABE=40°+2∠ABE.在△BDC中,BD=BC,
∴∠BDC+∠BCD+∠DBC=2β+40°+2∠ABE=180°.
∴β=70° - ∠ABE.
∴α+β=40°+∠ABE+70° - ∠ABE=110°.
∴∠BEC+∠BDC=110°.

24. (10分)(1)小新遇到这样一个问题:
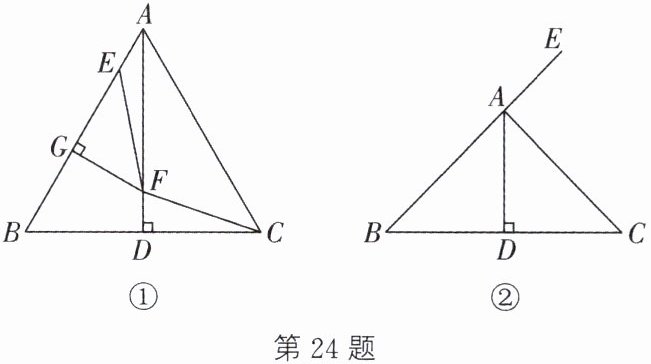
如图①,在等边三角形$ABC$中,$AD \perp BC于点D$,$E为AB$上一点,$BE的垂直平分线交AD于点F$,交$AB于点G$,连接$EF$,$FC$. 求$\angle EFC$的度数.
小新思考后发现,可以用两种方法解决问题:
方法一:通过运用线段垂直平分线的性质定理直接计算可解决问题.
方法二:过点$F作FM \perp AC于点M$,构造全等三角形可解决问题.
请你选择以上两种方法中的一种方法完成上述问题.
(2)参考小新思考问题的方法,解决下面的问题:
如图②,在$\triangle ABC$中,$AB = AC$,$AD \perp BC于点D$,$E为BA$延长线上的一点,$BE的垂直平分线交AD于点F$,交$AB于点G$,连接$EF$,$FC$,$CE$. 猜想$\angle CAD与\angle FCE$的数量关系,补全图形并加以证明.

答案：

(1)答案不唯一,如选择方法一:如图①,连接BF并延长，交AC于点H.
∵FG是BE的垂直平分线，
∴FE=FB.
∴∠FEB=∠FBE.
∴∠HFE=∠FEB+∠FBE=2∠FBE.
∵△ABC为等边三角形，AD⊥BC,
∴BD=CD.
∴FD是BC的垂直平分线.
∴FB=FC.
∴∠FBC=∠FCB.
∴∠HFC=∠FBC+∠FCB=2∠FBC.
∴∠EFC=∠HFE+∠HFC=2(∠FBE+∠FBC)=2∠ABC.
∵△ABC为等边三角形，
∴∠ABC=60°.
∴∠EFC=120°.
(2)∠CAD=∠FCE.补全图形如图②,连接BF,设EF交AC于点M.由
(1)，易知EF=BF=CF.
∴∠FEB=∠FBE,∠FBC=∠FCB,∠FEC=∠FCE.
∵AB=AC,
∴∠ABC=∠ACB.
∴∠ABC - ∠FBC=∠ACB - ∠FCB,即∠FBE=∠FCA.
∴∠FEB=∠FCA.
∵∠FEB+∠AME+∠MAE=180°,∠FCA+∠FMC+∠EFC=180°,∠AME=∠FMC,
∴∠MAE=∠EFC.
∵∠BAD+∠CAD+∠EAC=180°,∠FEC+∠FCE+∠EFC=180°,
∴∠BAD+∠CAD=∠FEC+∠FCE.
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD.又
∵∠FEC=∠FCE,
∴2∠CAD=2∠FCE,即∠CAD=∠FCE.