《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

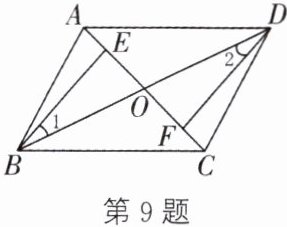
9. 新考法 开放题 如图,在四边形$ABCD$中,对角线$AC$,$BD相交于点O$,点$E$,$F分别在OA$,$OC$上。
(1)给出下列条件：①$OB= OD$；②$\angle 1= \angle 2$；③$OE= OF$。请你从中选择两个条件证明$\triangle BEO\cong\triangle DFO$。
(2)在(1)中你所选条件的前提下,添加$AE= CF$,求证：四边形$ABCD$是平行四边形。

答案：
(1)答案不唯一，如选择①②. 在△BEO和△DFO中，$\left\{\begin{array}{l} ∠1=∠2\\ OB=OD\\ ∠EOB=∠FOD\end{array}\right.$，
∴△BEO≌△DFO.
(2)由
(1)，知△BEO≌△DFO，
∴EO=FO.
∵AE=CF，
∴EO+AE=FO+CF，即AO=CO. 又
∵OB=OD，
∴四边形ABCD是平行四边形.

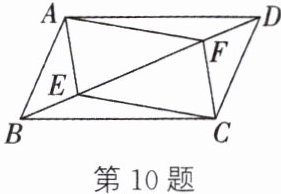
10. (内江中考)如图,在$□ ABCD$中,点$E$,$F在对角线BD$上,且$BE= DF$。求证：
(1)$\triangle ABE\cong\triangle CDF$；
(2)四边形$AECF$是平行四边形。

答案：
(1)
∵四边形ABCD是平行四边形，
∴AB=CD，AB//CD.
∴∠ABD=∠CDB. 在△ABE和△CDF中，$\left\{\begin{array}{l} AB=CD\\ ∠ABE=∠CDF\\ BE=DF\end{array}\right.$，
∴△ABE≌△CDF.
(2)由
(1)，可知△ABE≌△CDF，
∴AE=CF，∠AEB=∠CFD.
∴180°−∠AEB=180°−∠CFD，即∠AEF=∠CFE.
∴AE//CF.
∵AE=CF，AE//CF，
∴四边形AECF是平行四边形.

11. (无锡中考)如图,在$□ ABCD$中,$O为对角线BD$的中点,$EF过点O$,且分别交$AB$,$DC于点E$,$F$,连接$DE$,$BF$。求证：
(1)$\triangle DOF\cong\triangle BOE$；
(2)$DE= BF$。

答案：
(1)
∵O为对角线BD的中点，
∴OD=OB.
∵四边形ABCD是平行四边形，
∴DF//EB.
∴∠DFE=∠BEF. 在△DOF和△BOE中，$\left\{\begin{array}{l} ∠DFO=∠BEO\\ ∠DOF=∠BOE\\ OD=OB\end{array}\right.$，
∴△DOF≌△BOE.
(2)由
(1)，知△DOF≌△BOE，
∴DF=BE.
∵DF//EB，
∴四边形DFBE是平行四边形.
∴DE=BF.

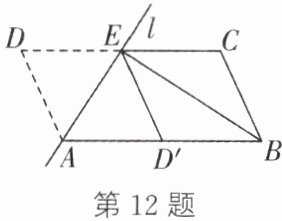
12. 如图,将$□ ABCD沿过点A的直线l$折叠,使点$D落到边AB上的点D'$处,直线$l交边CD于点E$,连接$BE$。
(1)求证：四边形$BCED'$是平行四边形；
(2)若$BE平分\angle ABC$,求证：$AB^2= AE^2+BE^2$。

答案：
(1)
∵四边形ABCD是平行四边形，
∴AB//CD，∠D=∠ABC. 由折叠，可知∠D=∠AD'E.
∴∠AD'E=∠ABC.
∴ED'//BC. 又
∵CE//BD'，
∴四边形BCED'是平行四边形.
(2)
∵BE平分∠ABC，
∴∠CBE=∠D'BE=$\frac{1}{2}$∠CBD'.
∵四边形ABCD是平行四边形，
∴AD//BC.
∴∠DAB+∠CBD'=180°. 由折叠，可知∠DAE=∠EAB=$\frac{1}{2}$∠DAB.
∴∠EAB+∠EBD'=$\frac{1}{2}$(∠DAB+∠CBD')=90°.
∴∠AEB=90°.
∴在Rt△ABE中，由勾股定理，得$AB^{2}=AE^{2}+BE^{2}$.