《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

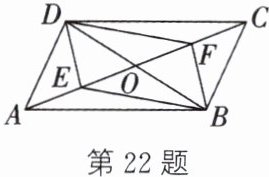
22.(6 分)(十堰中考)如图,在$□ ABCD$中,AC,BD 相交于点 O,E,F 分别是 OA,OC 的中点,连接 DE,DF,BE,BF.
(1)求证：$BE= DF$.
(2)设$\frac{AC}{BD}= k$. 当 k 为何值时,四边形 DEBF 是矩形？请说明理由.

答案： （1）
∵ 四边形ABCD是平行四边形，
∴ OB=OD，OA=OC.
∵ E，F分别为OA，OC的中点，
∴ OE=$\frac{1}{2}$OA，OF=$\frac{1}{2}$OC.
∴ OE=OF. 又
∵ OB=OD，
∴ 四边形DEBF是平行四边形.
∴ BE=DF. （2）当k=2时，四边形DEBF是矩形. 理由：
∵ $\frac{AC}{BD}=2$，
∴ AC=2BD. 由（1），得OE=$\frac{1}{2}$OA，OF=$\frac{1}{2}$OC，四边形DEBF是平行四边形，
∴ EF=$\frac{1}{2}$（OA+OC）=$\frac{1}{2}$AC，即AC=2EF.
∴ EF=BD.
∴ 四边形DEBF是矩形.

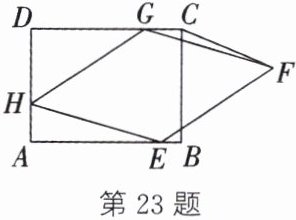
23.(8 分)如图,在矩形 ABCD 中,$AD= 6$,$CD= 8$,菱形 EFGH 的三个顶点 E,G,H 分别在矩形 ABCD 的边 AB,CD,DA 上,$AH= 2$,连接 CF.
(1)当$DG= 2$时,求证：四边形 EFGH 是正方形；
(2)当$△FCG$的面积为 2 时,求 DG 的长.

答案： （1）
∵ 四边形ABCD是矩形，
∴ ∠A=∠D=90°.
∴ ∠DGH+∠DHG=90°.
∵ 四边形EFGH是菱形，
∴ EH=GH.
∵ AH=2，DG=2，
∴ AH=DG.
∴ Rt△AEH≌Rt△DHG.
∴ ∠AHE=∠DGH.
∵ ∠DGH+∠DHG=90°，
∴ ∠AHE+∠DHG=90°.
∴ ∠EHG=90°.
∴ 四边形EFGH是正方形. （2）如图，过点F作FQ⊥DC，交DC的延长线于点Q，连接EG，则∠Q=90°.
∴ ∠A=∠Q=90°. 由矩形和菱形的性质，知AB//DC，HE//GF，
∴ ∠AEG=∠QGE，∠HEG=∠FGE.
∴ ∠AEH=∠QGF.
∵ EH=GF，
∴ △AEH≌△QGF.
∴ AH=QF=2.
∵ $S_{\triangle FCG}=\frac{1}{2}CG\cdot QF=\frac{1}{2}CG×2=2$，
∴ CG=2.
∴ DG=CD - CG=6.

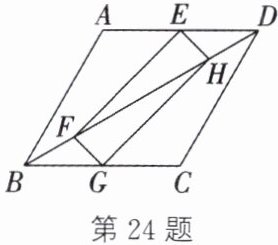
24.(8 分)如图,矩形 EFGH 的顶点 E,G 分别在菱形 ABCD 的边 AD,BC 上,顶点 F,H 在菱形 ABCD 的对角线 BD 上.
(1)求证：$BG= DE$.
(2)若 E 为 AD 的中点,$FH= 4$.
①求菱形 ABCD 的边长；
②若$∠ABC= 60^{\circ}$,求菱形 ABCD 的面积.

答案： （1）
∵ 四边形EFGH是矩形，
∴ GF=EH，EH//GF.
∴ ∠GFH=∠EHF.
∵ ∠BFG=180° - ∠GFH，∠DHE=180° - ∠EHF，
∴ ∠BFG=∠DHE.
∵ 四边形ABCD是菱形，
∴ AD//BC.
∴ ∠GBF=∠EDH. 在△BGF和△DEH中，$\left\{\begin{array}{l} ∠BFG=∠DHE,\\ ∠GBF=∠EDH,\\ GF=EH,\end{array}\right.$
∴ △BGF≌△DEH.
∴ BG=DE. （2）①如图①，连接EG.
∵ 四边形ABCD是菱形，
∴ AD//BC，AD=BC.
∵ E为AD的中点，
∴ AE=ED. 由（1），得BG=DE，
∴ AE//BG，AE=BG.
∴ 四边形ABGE是平行四边形.
∴ AB=EG.
∵ 四边形EFGH是矩形，
∴ EG=FH=4.
∴ AB=4.
∴菱形ABCD的边长为4. ②如图②，连接AC，AC与BD交于点O.
∵ 四边形ABCD是菱形，∠ABC=60°，
∴ ∠ABO=30°，AC⊥BD，OA=OC，OB=OD.
∴ 在Rt△ABO中，OA=$\frac{1}{2}$AB=2.
∴ AC=2OA=4.
∴ OB=$\sqrt{AB^2 - OA^2}=\sqrt{4^2 - 2^2}=2\sqrt{3}$.
∴ BD=2OB=4$\sqrt{3}$.
∴ 菱形ABCD的面积=$\frac{1}{2}AC\cdot BD=\frac{1}{2}×4×4\sqrt{3}=8\sqrt{3}$.