《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

10. 若$(m - 2)x^{|3 - m|} + 2≤6$是关于x的一元一次不等式,则$m = $______,不等式的解集为______.

答案： 4 x ≤ 2

11. 已知一次函数$y = ax + b$(a,b是常数),x与y的部分对应值如下表：
|x| -2| -1| 0| 1| 2| 3|
|y| 6| 4| 2| 0| -2| -4|
不等式$ax + b ＞ 0$的解集是______.

答案： x ＜ 1

12. 关于x的不等式$2x - m ＜ -1$的解集在数轴上表示如图所示,则m的值为______.

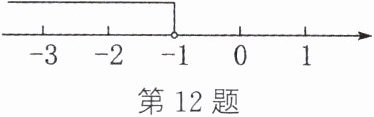
答案： - 1

13. (苏州中考)若$2x + y = 1$,且$0 ＜ y ＜ 1$,则x的取值范围是______.

答案： 0 ＜ x ＜ $\frac{1}{2}$

14. (龙东地区中考)若关于x的一元一次不等式组$\begin{cases}2x - 1 ＜ 3, \\ x - a ＜ 0\end{cases} 的解集为x ＜ 2$,则a的取值范围是______.

答案： a ≥ 2

15. 同时满足不等式$\frac{1 + 2x}{3} ＞ x - 1和x + 3(x - 1) ＜ 1$的x的最大整数是______.

答案： 0

16. 老师在黑板上留了一道解不等式的题目：$\frac{x + 2}{2}≥\frac{2x - 1}{3} + ☆$.☆是被一名学生擦去的一个数字,又知其解集为$x≤2$,则被擦去的数字是______.

答案： 1

17. 新情境 日常生活 如图所示为由若干个粗细均匀的铁环最大限度地拉伸组成的链条.已知铁环粗1cm,每个铁环长5cm.设铁环间处于最大限度的拉伸状态.若要组成不短于2m长的链条,则至少需要______个铁环.

答案： 66 解析:设需要x个铁环。2m = 200cm。依题意,得5x - 2(x - 1) ≥ 200,解得x ≥ 66。

18. (6分)解不等式(组),并将解集在数轴上表示出来.
(1)$\frac{2x - 1}{4} - \frac{1 + x}{6}≥1$；
(2)$\begin{cases}5x - 1≤3(x + 1)①, \\ \frac{2x - 1}{3} - \frac{2x + 3}{2} ＜ -1②.\end{cases} $

答案：
(1)x ≥ $\frac{17}{4}$。不等式的解集在数轴上表示如图①所示。
(2)解不等式①,得x ≤ 2,解不等式②,得x ＞ - 2.5。
∴原不等式组的解集为 - 2.5 ＜ x ≤ 2。不等式组的解集在数轴上表示如图②所示。

19. (6分)(扬州中考)解不等式组$\begin{cases}x - 2≤2x①, \\ x - 1 ＜ \frac{1 + 2x}{3}②,\end{cases} $并求出它的所有整数解的和.

答案： 解不等式①,得x ≥ - 2,解不等式②,得x ＜ 4。
∴原不等式组的解集是 - 2 ≤ x ＜ 4。
∴该不等式组的整数解是 - 2, - 1,0,1,2,3。
∵ - 2+( - 1)+0+1+2+3 = 3,
∴该不等式组的所有整数解的和是3。

20. (6分)已知方程组$\begin{cases}y - 2x = m, \\ 2y + 3x = m + 1\end{cases} 的解满足2x + y≥0$,求m的取值范围.

答案： 解方程组,得$\begin{cases}x = \frac{- m + 1}{7}\\y = \frac{5m + 2}{7}\end{cases}$。
∵2x + y ≥ 0,
∴2×$\frac{- m + 1}{7}$ + $\frac{5m + 2}{7}$ ≥ 0,解得m ≥ - $\frac{4}{3}$。