《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

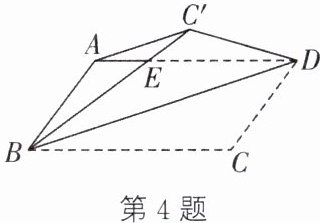
4. 如图,把平行四边形纸片$ABCD沿BD$折叠,点$C落在点C'$处,$BC'与AD相交于点E$。
(1)连接$AC'$,则$AC'与BD$的位置关系是______。
(2)$BE与DE$相等吗？证明你的结论。

答案：
(1)AC'//BD.
(2)BE与DE相等. 由折叠，得∠CBD=∠C'BD.
∵四边形ABCD是平行四边形，
∴AD//BC.
∴∠ADB=∠CBD.
∴∠EDB=∠EBD，
∴BE=DE.

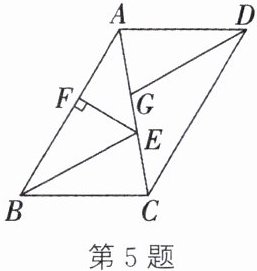
5. (扬州中考)如图,在$□ ABCD$中,$BE$,$DG分别平分\angle ABC$,$\angle ADC$,交$AC于点E$,$G$。
(1)求证：$DG// BE$,$DG= BE$。
(2)过点$E作EF\perp AB$,垂足为$F$。若$□ ABCD$的周长为56,$EF= 6$,求$\triangle ABC$的面积。

答案：

(1)
∵四边形ABCD是平行四边形，
∴AD//BC，AD=BC，AB=CD，∠ABC=∠ADC.
∴∠DAC=∠BCA.
∵BE，DG分别平分∠ABC，∠ADC，
∴∠CBE=$\frac{1}{2}$∠ABC，∠ADG=$\frac{1}{2}$∠ADC，
∴∠ADG=∠CBE.
∵∠DGE=∠DAC+∠ADG，∠BEG=∠BCA+∠CBE，
∴∠DGE=∠BEG.
∴DG//BE. 在△ADG和△CBE中，$\left\{\begin{array}{l} ∠DAG=∠BCE\\ AD=CB\\ ∠ADG=∠CBE\end{array}\right.$，
∴△ADG≌△CBE.
∴DG=BE.
(2)如图，过点E作EH⊥BC于点H.
∵BE平分∠ABC，EF⊥AB，EH⊥BC，
∴EH=EF=6.
∵▱ABCD的周长为56，
∴AB+BC=28.
∴$S_{\triangle ABC}=\frac{1}{2}AB\cdot EF+\frac{1}{2}BC\cdot EH=\frac{1}{2}EF\cdot (AB+BC)=\frac{1}{2}×6×28=84$.

6. $^\star$在平面直角坐标系中,以$A(0,2)$,$B(-1,-1)$,$C(3,0)$,$D$为顶点构造平行四边形。下列不能作为顶点$D$的坐标是( )

A.$(2,-3)$
B.$(-4,1)$
C.$(4,3)$
D.$(-4,0)$

答案： D

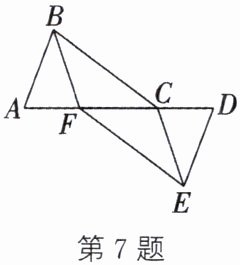
7. (河池中考)如图,点$A$,$F$,$C$,$D$在同一条直线上,$AB= DE$,$AF= CD$,$BC= EF$。
(1)求证：$\angle ACB= \angle DFE$；
(2)连接$BF$,$CE$,直接判断四边形$BFEC$的形状。

答案：
(1)
∵AF=CD，
∴AF+CF=CD+CF，即AC=DF. 在△ABC和△DEF中，$\left\{\begin{array}{l} AB=DE\\ BC=EF\\ AC=DF\end{array}\right.$，
∴△ABC≌△DEF.
∴∠ACB=∠DFE.
(2)四边形BFEC是平行四边形. 解析:由
(1)，可知∠ACB=∠DFE，
∴BC//EF. 又
∵BC=EF，
∴四边形BFEC是平行四边形.

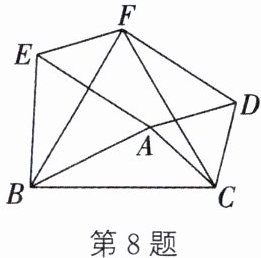
8. 如图,以$\triangle ABC的三边为边分别作等边三角形ACD$,等边三角形$ABE$,等边三角形$BCF$,连接$EF$,$FD$。求证：四边形$ADFE$是平行四边形。

答案：
∵△ABE，△BCF为等边三角形，
∴AB=BE=AE，BC=CF=FB，∠ABE=∠CBF=60°.
∴∠ABE−∠ABF=∠CBF−∠ABF，即∠FBE=∠CBA. 在△EBF和△ABC中，$\left\{\begin{array}{l} EB=AB\\ ∠FBE=∠CBA\\ BF=BC\end{array}\right.$，
∴△EBF≌△ABC.
∴EF=AC. 又
∵△ACD为等边三角形，
∴CD=AD=AC.
∴EF=AD. 同理，可证△ABC≌△DFC，
∴AB=DF.
∴DF=AE.
∴四边形ADFE是平行四边形.