第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1. 数形结合思想 如图,直线$y= 2x与y= kx+b相交于点P(m,2)$,则关于x的方程$kx+b= 2$的解是 ( )

A.$x= \frac{1}{2}$
B.$x= 1$
C.$x= 2$
D.$x= 4$

A.$x= \frac{1}{2}$
B.$x= 1$
C.$x= 2$
D.$x= 4$
答案:
B
2. 如图,点$A(0,4),C(-2,0)在直线l:y= kx+b$上,直线l和函数$y= -4x+a$的图象交于点B.
(1) 求直线l对应的函数表达式;
(2) 若点B的横坐标是1,求关于x,y的方程组$\left\{\begin{array}{l} y= kx+b,\\ y= -4x+a\end{array} \right. $的解及a的值.
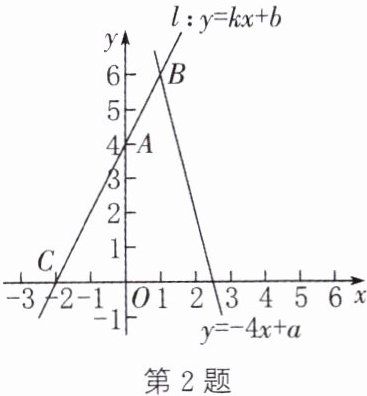
(1) 求直线l对应的函数表达式;
(2) 若点B的横坐标是1,求关于x,y的方程组$\left\{\begin{array}{l} y= kx+b,\\ y= -4x+a\end{array} \right. $的解及a的值.

答案:
(1)
∵点A(0,4),C(-2,0)在直线l:y=kx+b上,
∴{b=4,-2k+b=0,解得{k=2,b=4.
∴直线l对应的函数表达式为y=2x+4.(2)
∵点B的横坐标是1,且在直线l上,
∴当x=1时,y=2+4=6.
∴点B的坐标为(1,6).
∵点B是直线l与直线y=-4x+a的交点,
∴关于x,y的方程组{y=kx+b,y=-4x+a的解为{x=1,y=6.把x=1,y=6代入y=-4x+a,得-4+a=6,解得a=10.
∵点A(0,4),C(-2,0)在直线l:y=kx+b上,
∴{b=4,-2k+b=0,解得{k=2,b=4.
∴直线l对应的函数表达式为y=2x+4.(2)
∵点B的横坐标是1,且在直线l上,
∴当x=1时,y=2+4=6.
∴点B的坐标为(1,6).
∵点B是直线l与直线y=-4x+a的交点,
∴关于x,y的方程组{y=kx+b,y=-4x+a的解为{x=1,y=6.把x=1,y=6代入y=-4x+a,得-4+a=6,解得a=10.
3. 直线$y= kx+b$与两坐标轴的交点如图所示,当$y<0$时,x的取值范围是 ( )

A.$x>2$
B.$x<2$
C.$x>-1$
D.$x<-1$

A.$x>2$
B.$x<2$
C.$x>-1$
D.$x<-1$
答案:
B
4. (娄底中考)如图,直线$y= x+b和y= kx+4$与x轴分别相交于点$A(-4,0),B(2,0)$,则关于x的不等式组$\left\{\begin{array}{l} x+b>0,\\ kx+4>0\end{array} \right. $的解集为( )

A.$-4<x<2$
B.$x<-4$
C.$x>2$
D.$x<-4或x>2$

A.$-4<x<2$
B.$x<-4$
C.$x>2$
D.$x<-4或x>2$
答案:
A
5. (扬州中考)如图,函数$y= kx+b(k<0)$的图象经过点P,则关于x的不等式$kx+b>3$的解集为____.


答案:
x<-1
6. 如图,直线$y= -x+m与y= x+4$交点的横坐标为-2,则关于x的不等式组$-x+m>x+4>0$的解集为____.
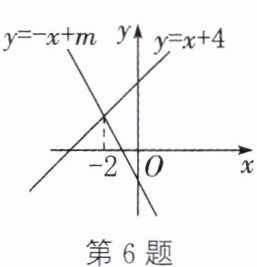

答案:
-4<x<-2
查看更多完整答案,请扫码查看


