《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

典例3 (泰州中考)如图,线段DE与AF分别为△ABC的中位线与中线.
(1) 求证：AF与DE互相平分.
(2) 当线段AF与BC满足怎样的数量关系时,四边形ADFE为矩形？请说明理由.

点拨 (1) 根据线段中点的定义可得$AD= \frac {1}{2}AB,$根据三角形的中位线定理可得EF//AB,$EF= \frac {1}{2}AB,$从而可得EF= AD,进而可得四边形ADFE是平行四边形,然后利用平行四边形的性质即可解答；(2) 当$AF= \frac {1}{2}BC$时,四边形ADFE为矩形,再根据三角形的中位线定理可得$DE= \frac {1}{2}BC,$从而可得AF= DE,然后利用(1)的结论即可解答.
解答：
解有所悟：证明矩形的思路有两种. 思路一：若已知四边形是平行四边形,则只要再证明一个角是直角或再证明两条对角线相等即可. 思路二：若没有平行四边形的条件,则考虑证明三个角是直角,直接得到矩形或先证明四边形是平行四边形,再按思路一证明即可.

答案： （1）
∵ 线段 DE 与 AF 分别为△ABC 的中位线与中线，
∴ D 是 AB 的中点，E 是 AC 的中点，F 是 BC 的中点.
∴ AD=$\frac{1}{2}$AB，EF 是△ABC 的中位线.
∴ EF//AB，EF=$\frac{1}{2}$AB.
∴ EF=AD.
∴ 四边形 ADFE 是平行四边形.
∴ AF 与 DE 互相平分.（2）当 AF=$\frac{1}{2}$BC 时，四边形 ADFE 为矩形. 理由：
∵ 线段 DE 为△ABC 的中位线，
∴ DE=$\frac{1}{2}$BC.
∵ AF=$\frac{1}{2}$BC，
∴ AF=DE. 由（1），得四边形 ADFE 是平行四边形，
∴ 四边形 ADFE 为矩形.

1. 下列结论中,矩形具有而菱形不一定具有的性质是( )

A.对边平行且相等
B.对角线互相平分
C.对角线相等
D.对角线互相垂直

答案： C

2. (聊城中考)要检验一个四边形的桌面是否为矩形,可行的测量方案是( )

A.测量两条对角线是否相等
B.度量两个角是否是90°
C.测量两条对角线的交点到四个顶点的距离是否相等
D.测量两组对边是否分别相等

答案： C

3. (永州中考)如图,在Rt△ABC中,∠ABC= 90°,∠C= 60°,D为边AC的中点,BD= 2,则BC的长为$( )A. \sqrt {3}B. 2\sqrt {3}C. 2D. 4$

答案： C

4. 如图,在矩形ABCD中,对角线AC与BD相交于点O,E,F分别是AB,AO的中点,且AC= 8,则EF的长为( )

A.2
B.4
C.6
D.8

答案： A

5. (邵阳中考)已知矩形的一边长为6cm,一条对角线的长为10cm,则该矩形的面积为$______cm^{2}.$

答案： 48

6. 如图,在四边形ABCD中,AB//DC,AD//BC,在不添加任何辅助线的前提下,要想使四边形ABCD成为一个矩形,只需要添加的一个条件是______.

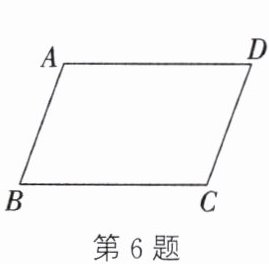
答案： 答案不唯一，如∠A=90°