《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

9. ★如图,$P为定角\angle AOB$的平分线上的一个定点,且$\angle MPN与\angle AOB$互补. 若$\angle MPN在绕点P$旋转的过程中,其两边分别与$OA$,$OB相交于M$,$N$两点,连接$MN$,有下列结论:①$PM = PN$恒成立;②$OM + ON$的值不变;③四边形$PMON$的面积不变;④$MN$的长不变. 其中,正确的个数为( )

A.$4$
B.$3$
C.$2$
D.$1$

答案：
9.B　解析:如图,过点P作PE⊥OA于点E,PF⊥OB于点F.
∴∠PEO=∠PFO=90°.
∴∠EPF+∠AOB=180°.
∵∠MPN+∠AOB=180°,
∴∠EPF=∠MPN.
∴∠EPF - ∠EPN=∠MPN - ∠EPN,即∠FPN=∠EPM.
∵OP平分∠AOB,PE⊥OA,PF⊥OB,
∴PE=PF.在Rt△POE和Rt△POF中,{OP=OP,PE=PF},
∴Rt△POE≌Rt△POF.
∴OE=OF.在△PEM和△PFN中,{∠MPE=∠NPF,PE=PF,∠PEM=∠PFN=90°},
∴△PEM≌△PFN.
∴EM=FN,PM=PN,故①正确.
∵△PEM≌△PFN,
∴S△PEM=S△PFN.
∴S四边形PMON=S四边形PEOF=定值，故③正确.
∵OM+ON=OE+ME+OF - NF=2OE,
∴OM+ON=定值，故②正确.易知MN的长是变化的，故④错误.综上所述，正确的个数为3.
方法点金：角平分线的性质与判定的技巧：技巧1:角平分线上的点到角两边的距离相等,即垂线段相等,以两垂线段为高的等底三角形的面积相等.技巧2:解决角平分线的相关问题,常需要添加辅助线,构造角平分线性质、判定的基本图形,以利用其性质与判定解决问题.技巧3:三角形的三条角平分线交于一点(内心),这一点到三角形三边的距离相等,解决相关问题常需要过此交点作三角形边的垂线段,进而利用此性质解决问题.
　　　

10. 命题“直角三角形的两个锐角互余”的逆命题是______,这个逆命题是______(填“真”或“假”)命题.

答案： 如果一个三角形有两个锐角，且这两个锐角互余，那么这个三角形是直角三角形　真

11. ★已知$\triangle ABC$是等腰三角形. 若$\angle A = 40^{\circ}$,则$\triangle ABC$的顶角度数是______.

答案： 40°或100°
易错题提示：因未正确运用分类讨论解题而导致漏解。解答这类问题时,要根据条件正确进行分类,这类问题中没有明确顶角或底角的度数,解题时要注意分情况讨论.本题没有明确哪个角是等腰三角形的顶角,需要分∠A是顶角、∠A是底角两种情况进行讨论,再根据等腰三角形的性质和内角和定理求解.

12. (嘉兴中考)小明同学复习时将几种三角形的关系整理如图,请帮他在括号内填上一个适当的条件:______.

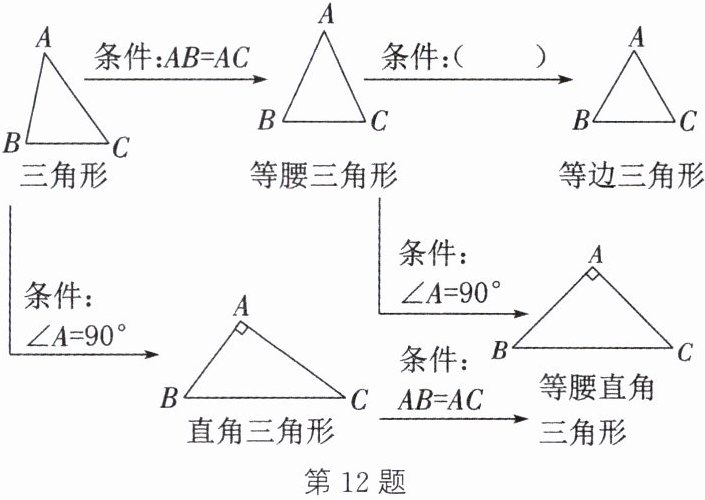
答案： 答案不唯一,如∠B=60°

13. (常德中考)如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AD平分\angle CAB$,$DE \perp AB于点E$. 若$CD = 3$,$BD = 5$,则$BE$的长为______.

答案： 4

14. 如图,在等腰三角形$ABC$中,$AB = AC$,$\angle BAC = 80^{\circ}$,$AD \perp BC$,$AD = AB$,连接$BD$并延长,交$AC的延长线于点E$,则$\angle E$的度数是______.

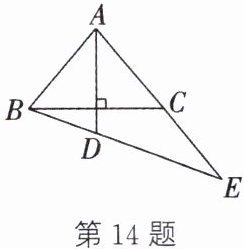
答案： 30°

15. (陕西中考)如图,在$\text{Rt} \triangle ABC$中,$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,$AB = 8$. 若$E$,$F是边BC$上的两个动点,以$EF为边的等边三角形EFP的顶点P在\triangle ABC$的内部或边上,则等边三角形$EFP$的周长的最大值为______.

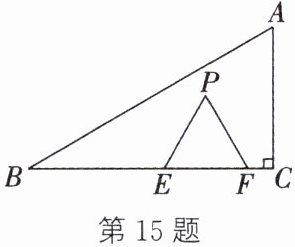
答案： 6√3

16. (鄂尔多斯中考)如图,$AB \perp BC于点B$,$AB \perp AD于点A$,$E是CD$的中点. 若$BC = 5$,$AD = 10$,$BE = \frac{13}{2}$,则$AB$的长是______.

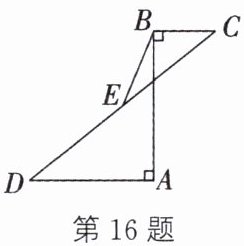
答案：
12　解析:如图,延长BE交AD于点F.
∵E是CD的中点，
∴DE=CE.
∵AB⊥BC,AB⊥AD,
∴易得AD//BC.
∴∠D=∠C.
∵∠FED=∠BEC,
∴△FDE≌△BCE.
∴DF=CB=5,FE=BE.
∴AF=AD - DF=5,BF=2BE=13.在Rt△ABF中,由勾股定理，可得AB=12.
　　

17. ★如图,在$\triangle ABC$中,$AB$,$AC的垂直平分线l_{1}$,$l_{2}相交于点O$. 若$\angle BAC = 76^{\circ}$,则$\angle OBC$的度数为______.

答案：
14°　解析:如图,连接OA.
∵AB,AC的垂直平分线l₁,l₂相交于点O,
∴OA=OB,OA=OC.
∴∠OBA=∠OAB,∠OCA=∠OAC,OB=OC.
∴∠OBA+∠OCA=∠OAB+∠OAC=∠BAC.
∵∠BAC=76°,
∴∠OBA+∠OCA=76°.
∴∠OBC+∠OCB=180° - ∠BAC - (∠OBA+∠OCA)=28°.
∵OB=OC,
∴∠OBC=∠OCB=14°.
方法点金：线段垂直平分线的性质与判定的技巧：技巧1:直接运用线段垂直平分线的性质可进行等线段转移,在求三角形的周长时,可将三角形的周长转化为两条线段的和,进而解决问题.技巧2:由线段垂直平分线的性质得等线段,由等线段得到等角,即等边对等角,进而结合三角形的内角和定理可解决相关问题.技巧3:三角形的三边的垂直平分线交于一点(三角形的外心),由两边的垂直平分线相交即可确定这一点,这一点到三角形三个顶点的距离都相等,解决问题时,常连接这一点与三角形的顶点,进而利用三角形的性质巧解问题.
　　　

18. (6分)如图,在$\triangle ABC$中,$AC = BC$,直线$l经过顶点C$,过$A$,$B两点分别作直线l的垂线AE$,$BF$,垂足分别为$E$,$F$,且$AE = CF$. 求证:$\angle ACB = 90^{\circ}$.

答案：
∵AE⊥EF,BF⊥EF,
∴∠AEC=∠CFB=90°.在Rt△ACE和Rt△CBF中,{AC=CB,AE=CF},
∴Rt△ACE≌Rt△CBF.
∴∠EAC=∠FCB.
∵∠AEC=90°,
∴∠EAC+∠ACE=90°.
∴∠ACE+∠FCB=90°.
∵E,C,F三点都在直线l上,
∴∠ACB=180° - (∠ACE+∠FCB)=180° - 90°=90°.