《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

9.(遂宁中考)若关于 $x$ 的方程 $\frac{2}{x} = \frac{m}{2x + 1}$ 无解,则 $m$ 的值为( )

A.$0$
B.$4$ 或 $6$
C.$6$
D.$0$ 或 $4$

答案： D

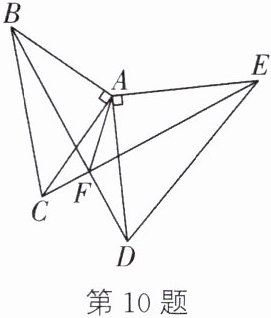
10. 如图,$\triangle ABC$ 和 $\triangle ADE$ 都是等腰直角三角形,$\angle BAC = \angle DAE = 90^{\circ}$,$BD$,$CE$ 交于点 $F$,连接 $AF$. 有下列结论：① $BD = CE$；② $BD \perp CE$；③ $AF$ 平分 $\angle CAD$；④ $\angle AFE = 45^{\circ}$. 其中,正确的有( )

A.$1$ 个
B.$2$ 个
C.$3$ 个
D.$4$ 个

答案：
C 解析:如图,过点 A 作 AM⊥BD 于点 M,AN⊥EC 于点 N,设 CE 交 AD 于点 O.
∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
∵△ABC 和△ADE 都是等腰直角三角形,
∴AB=AC,AD=AE.在△BAD 和△CAE 中,{AB=AC,∠BAD=∠CAE,AD=AE},
∴△BAD≌△CAE.
∴BD=CE,∠BDA=∠CEA. 故①正确.
∵∠DOF=∠AOE,∠BDA=∠CEA,
∴180° - ∠DOF - ∠BDA=180° - ∠AOE - ∠CEA,即∠DFO=∠EAO=90°.
∴BD⊥CE.故②正确.
∵△BAD≌△CAE,
∴S△BAD=S△CAE.
∴1/2BD·AM = 1/2CE·AN.
∵BD=CE,
∴AM=AN.又
∵AM⊥FB,AN⊥FE,
∴FA 平分∠EFB.
∴∠AFE=45°.故④正确.③无法证明其正确性.综上所述,正确的有 3 个.
　　　　　　　

11. 分解因式：$a^{2}(x - y) + (y - x) = $ ______.

答案： (x - y)(a + 1)(a - 1)

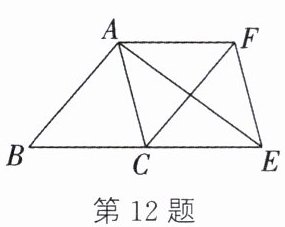
12. 如图,将 $\triangle ABC$ 沿 $BC$ 方向平移到 $\triangle FCE$ 的位置,连接 $AF$,$AE$,图中的平行四边形是______.

答案： □ABCF,□ACEF

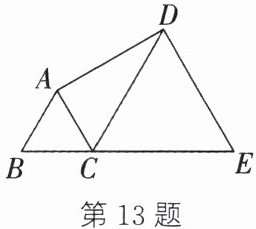
13. 如图,$\triangle ABC$ 与 $\triangle DCE$ 都是等边三角形,$B$,$C$,$E$ 三点在同一条直线上. 若 $AB = 3$,$\angle BAD = 150^{\circ}$,则 $DE$ 的长为______.

答案： 6

14. 若整数 $m$ 使得关于 $x$ 的不等式组 $\begin{cases} x + m ＜ 1 + \frac{3x + m}{2}, \\ 5x - 1 \leqslant 2(x + \frac{3}{2}) \end{cases} $ 有且只有两个整数解,则满足条件的 $m$ 的值为______.

答案： 1

15.(长春中考)为了让学生崇尚劳动,尊重劳动,在劳动中提升综合素质,某校定期开展劳动实践活动. 甲、乙两班在一次体验挖土豆的活动中,甲班挖 1500 千克土豆与乙班挖 1200 千克土豆所用的时间相同. 已知甲班平均每小时比乙班多挖 100 千克土豆,则乙班平均每小时挖______千克土豆.

答案： 400

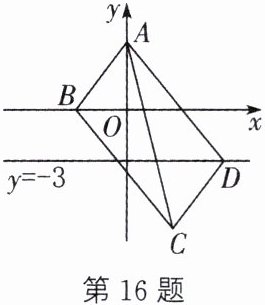
16. 如图,$□ ABCD$ 的顶点 $A$ 的坐标为 $(0, 4)$,顶点 $B$,$D$ 分别在 $x$ 轴和直线 $y = -3$ 上,则对角线 $AC$ 长的最小值为______.

答案：
11 解析:如图,连接 BD,设点 C 的坐标为(a,b).
∵顶点 B,D 分别在 x 轴和直线 y = -3 上,
∴点 B,D 的纵坐标分别为 0,-3.
∵四边形 ABCD 是平行四边形,
∴AC 与 BD 互相平分.
∴(-3 + 0)/2 = (4 + b)/2,
∴b = -7.
∴点 C 在直线 y = -7 上.
∴当 AC 垂直于直线 y = -7 时,AC 的长有最小值.
∴对角线 AC 长的最小值为 4 - (-7)=11.
　　　　　　　

17.(4 分)现有代数式：$9y^{2}$,$1$,$(2x + 3y)^{2}$. 请你从上述各式中任选两式作差,然后把这个式子进行因式分解.

答案： 答案不唯一,如9y² - 1=(3y - 1)(3y + 1).

18.(4 分)(威海中考)解不等式组 $\begin{cases} 4x - 2 \leqslant 3(x + 1) ①, \\ 1 - \frac{x - 1}{2} ＜ \frac{x}{4} ②, \end{cases} $ 并把解集在数轴上表示出来.

答案：
解不等式①,得x≤5,解不等式②,得x＞2.
∴原不等式组的解集为2＜x≤5.在数轴上表示不等式组的解集如图所示.