《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

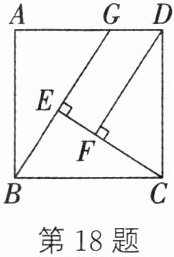
18.(6 分)(恩施中考)如图,四边形 ABCD 是正方形,G 为线段 AD 上任意一点,$CE⊥BG$于点 E,$DF⊥CE$于点 F. 求证：$DF= BE+EF$.

答案：
∵ 四边形ABCD是正方形，
∴ BC=CD，∠BCD=90°.
∵ CE⊥BG，DF⊥CE，
∴ ∠BEC=∠DFC=90°.
∴ ∠BCE+∠CBE=90°=∠BCE+∠DCF.
∴ ∠CBE=∠DCF. 在△CBE和△DCF中，$\left\{\begin{array}{l} ∠CBE=∠DCF,\\ ∠BEC=∠CFD,\\ BC=CD,\end{array}\right.$
∴ △CBE≌△DCF.
∴ BE=CF，CE=DF.
∵ CE=CF+EF，
∴ DF=BE+EF.

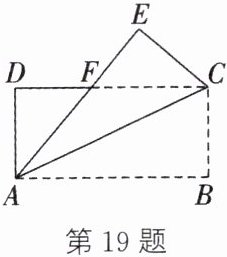
19.(6 分)(苏州中考)如图,将矩形 ABCD 沿对角线 AC 折叠,点 B 的对应点为 E,AE 与 CD 交于点 F.
(1)求证：$△DAF≌△ECF$；
(2)若$∠ECF= 40^{\circ}$,求$∠CAB$的度数.

答案： （1）将矩形ABCD沿对角线AC折叠，则AD=BC=EC，∠D=∠B=∠E=90°. 在△DAF和△ECF中，$\left\{\begin{array}{l} ∠DFA=∠EFC,\\ ∠D=∠E,\\ DA=EC,\end{array}\right.$
∴ △DAF≌△ECF. （2）由（1），得△DAF≌△ECF，
∴ ∠DAF=∠ECF=40°.
∵ 四边形ABCD是矩形，
∴ ∠DAB=90°.
∴ ∠EAB=∠DAB - ∠DAF=90° - 40°=50°. 由折叠，得∠EAC=∠CAB，
∴ ∠CAB=25°.

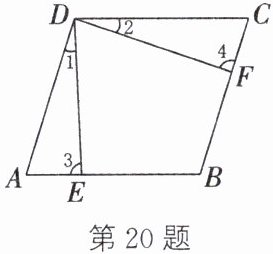
20.(6 分)(岳阳中考)如图,点 E,F 分别在$□ ABCD$的边 AB,BC 上,$AE= CF$,连接 DE,DF. 有以下三个条件：①$∠1= ∠2$；②$DE= DF$；③$∠3= ∠4$. 在这三个条件中,选择一个合适的作为已知条件,使$□ ABCD$为菱形.
(1)选择的条件是______(填序号)；
(2)根据(1)中选择的条件,求证：$□ ABCD$为菱形.

答案： （1）① （2）
∵ 四边形ABCD是平行四边形，
∴ ∠A=∠C. 在△ADE和△CDF中，$\left\{\begin{array}{l} ∠1=∠2,\\ ∠A=∠C,\\ AE=CF,\end{array}\right.$
∴ △ADE≌△CDF.
∴ AD=CD.
∴ □ABCD为菱形.

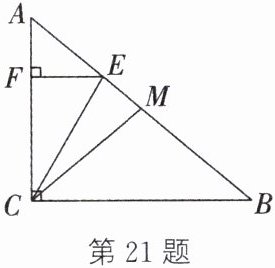
21.(6 分)(杭州中考)如图,在$Rt△ACB$中,$∠ACB= 90^{\circ}$,$∠A= 50^{\circ}$,M 为边 AB 的中点,点 E 在线段 AM 上,$EF⊥AC$于点 F,连接 CM,CE,$∠ACE= 30^{\circ}$.
(1)求证：$CE= CM$；
(2)若$AB= 4$,求线段 FC 的长.

答案： （1）
∵ ∠ACB=90°，M为边AB的中点，
∴ MC=MA=MB.
∴ ∠MCA=∠A，∠MCB=∠B.
∵ ∠A=50°，
∴ ∠MCA=50°.
∴ ∠MCB=∠B=90° - 50°=40°.
∴ ∠EMC=∠MCB+∠B=80°.
∵ ∠ACE=30°，
∴ ∠MEC=∠A+∠ACE=80°.
∴ ∠MEC=∠EMC.
∴ CE=CM. （2）
∵ AB=4，M为边AB的中点，
∴ CE=CM=$\frac{1}{2}$AB=2.
∵ EF⊥AC，∠ACE=30°，
∴ EF=$\frac{1}{2}$CE=1.
∴ FC=$\sqrt{CE^2 - EF^2}=\sqrt{2^2 - 1^2}=\sqrt{3}$.