《2025年通城学典暑期升级训练延边大学出版社八年级数学北师大版》

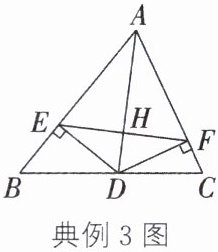
典例3(兴安盟中考)如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,连接EF,EF与AD相交于点H。
(1)求证：AD⊥EF。
(2)当△ABC满足什么条件时,四边形AEDF是正方形？请说明理由。

点拨(1)根据AAS证明△AED≌△AFD,进而利用全等三角形的性质及等腰三角形三线合一的性质解答即可；(2)根据对角线垂直的矩形是正方形,只需判断四边形AEDF是矩形即可解答。
解答：
解有所悟：在平行四边形、矩形或菱形的基础上添加相关条件就可以判断一个四边形是正方形。对于探究使一个图形是正方形的条件的问题,我们在求解时往往需要假设得到的四边形是正方形的情形下探究某些边或角所具有的关系,再由添加的条件来完成证明过程。

答案：
(1)
∵AD是△ABC的角平分线，
∴∠EAD=∠FAD.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.在△AED和△AFD中，$\begin{cases}∠EAD = ∠FAD\\∠AED = ∠AFD\\AD = AD\end{cases}$，
∴△AED≌△AFD.
∴AE=AF.
∴AD⊥EF.
(2)当△ABC满足∠BAC=90°时，四边形AEDF是正方形.理由:
∵∠AED=∠AFD=∠BAC=90°,
∴四边形AEDF 是矩形.由
(1)，得AD⊥EF,
∴四边形AEDF是正方形.

1. 下列说法中,正方形具有而矩形不具有的性质是( )

A.两组对边分别平行
B.对角线互相垂直
C.四个角都为直角
D.对角线互相平分

答案： B

2. (玉林中考)如图,一个四边形顺次添加下列条件中的三个条件便得到正方形：a.两组对边分别相等；b.一组对边平行且相等；c.一组邻边相等；d.一个角是直角。顺次添加的条件：①a→c→d；②b→d→c；③a→b→c。其中,正确的是( )

A.①
B.③
C.①②
D.②③

答案： C

3. (黄石中考)如图,正方形OABC的边长为√2,将正方形OABC绕原点O按顺时针方向旋转45°,则点B的对应点的坐标为( )

A.(-√2,0)
B.(√2,0)
C.(0,√2)
D.(0,2)

答案： D

4. (泰州中考)如图,P为AB上任意一点,分别以AP,PB为边在AB同侧作正方形APCD,正方形PBEF。设∠CBE= α,则∠AFP的度数为( )

A.2α
B.90°-α
C.45°+α
D.90°-1/2α

答案： B