《2025年时习之暑假衔接七年级数学北师大版》

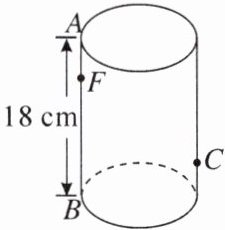
7.如图,圆柱形无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度。

答案：
解:将曲面沿AB展开，如图所示，过C作$CE⊥AB$于E.在$Rt△CEF$中，$∠CEF=90^{\circ }$，$EF=18 - 1 - 1 = 16(cm)$，$CE=\frac{1}{2}×60 = 30(cm)$.由勾股定理得$CF^{2}=CE^{2}+EF^{2}=30^{2}+16^{2}=34^{2}$，即$CF = 34cm$.答:蜘蛛所走的最短路线的长度是34cm.

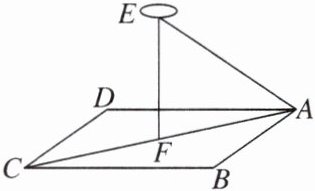
8.如图,某公司在门前长方形小广场ABCD上空放一氢气球,为使氢气球悬挂于广场中央F的正上方,公司欲从点A到气球E拉一根细绳,已知小广场宽AB= 18米,长BC= 24米,F为AC中点,气球高EF= 8米,求细绳AE的长。

答案： 解:在$Rt△ABC$中，$AB = 18$米，$BC = 24$米，则$AC^{2}=AB^{2}+BC^{2}=18^{2}+24^{2}=30^{2}$，所以$AC = 30$米.在$Rt△AEF$中，F为AC的中点，故$AF=\frac{1}{2}AC = 15$米，$EF = 8$米，$AE^{2}=AF^{2}+EF^{2}=15^{2}+8^{2}=289$，所以$AE = 17$米.

【综合实践】
【问题情境】消防云梯的作用是用于高层建筑火灾等救援任务,它能让消防员快速到达高层救援现场,如图,已知一架云梯AB长25m斜靠在一面墙上,这时云梯底端距墙角的距离OB= 20m,∠AOB= 90°.
【独立思考】(1)求这架云梯顶部距离地面OA的长度。
【深入探究】(2)消防员接到命令,按要求将云梯从顶部A下滑到A'位置上(云梯长度不改变),则底部B沿水平方向向前滑动到B'位置上,若AA'= 8m,求BB'的长度。
【问题解决】(3)在演练中,墙边距地面24m的窗口有求救声,消防员需调整云梯去救援被困人员。经验表明,云梯靠墙摆放时,若云梯底端离墙的距离不小于云梯长度的1/5,则云梯和消防员相对安全,在相对安全的前提下,云梯的顶端能否到达24m高的窗口去救援被困人员？

答案： 解:
(1)在直角三角形AOB中，$∠AOB = 90^{\circ }$，所以$OA^{2}=AB^{2}-OB^{2}=25^{2}-20^{2}=225$.所以$OA = 15m$.
(2)$AA' = 8m$，所以$A'O = OA - AA' = 7m$，$OB'^{2}=A'B'^{2}-A'O^{2}=25^{2}-7^{2}=576$.所以$OB' = 24m$.$\therefore BB' = OB' - OB = 4m$.
(3)$25×\frac{1}{5}=5m$，即$OB = 5m$.当$OB = 5m$时，$OA^{2}=AB^{2}-OB^{2}=600$，因为$24^{2}=576＜600$，所以能到达窗口去救援被困人员.