《2025年时习之暑假衔接七年级数学北师大版》

1.用简便方法计算下列各题．
(1)$999^{2}$；
(2)$650^{2} - 648×652$；
(3)$(2 + 1)(2^{2} + 1)(2^{4} + 1)(2^{8} + 1)(2^{16} + 1)$．

答案： 解:
(1)原式=(1000−1)²=1000²−2×1000×1+1²=998001.
(2)原式=650²−(650−2)×(650+2)=650²−(650²−4)=
　650²−650²+4=4.
(3)原式=(2−1)(2+1)(2²+1)(2+1)(28+1)(216+1)=
　(2²−1)(2²+1)(24+1)(28+1)(216+1)=(24−1)(24+1)(28+1)(216+1)=(28−1)(28+1)(2116+1)=(216−1)(216+1)=232−1.

例2 已知$(a - b)^{2}= 25$,$ab = - 6$,求下列各式的值．
(1)$a^{2} + b^{2}$；
(2)$a^{4} + b^{4}$．

答案： 【解答】
(1)因为$(a - b)^{2}= 25$,$ab = - 6$,所以$a^{2} + b^{2}= a^{2} + b^{2} - 2ab + 2ab= (a - b)^{2} + 2ab= 25 + 2×(-6)= 25 - 12= 13$．
(2)因为$a^{2} + b^{2}= 13$,$ab = - 6$,所以$a^{4} + b^{4}= (a^{2} + b^{2})^{2} - 2a^{2}b^{2}= 13^{2} - 2×(-6)^{2}= 169 - 72= 97$．

例3 如图,大正方形的边长为$a$,小正方形的边长为$b$,若$a + b = 7$,$ab = 11$,则阴影部分的面积为______．

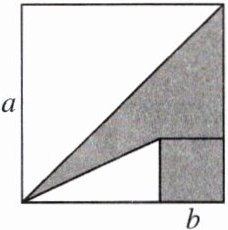
答案： 【解答】由图形中各个部分面积之间的关系可得,$S_{阴影部分}= \frac{1}{2}a^{2} - \frac{1}{2}b(a - b)= \frac{1}{2}a^{2} - \frac{1}{2}ab + \frac{1}{2}b^{2}= \frac{1}{2}(a^{2} - ab + b^{2})= \frac{1}{2}[(a + b)^{2} - 3ab]= \frac{1}{2}×(49 - 3×11)= 8$．

2.若$m + 98^{2} - 1= 102^{2}$,则$m$的值为()
A.100
B.799
C.800
D.801

答案： D

1.若$a - \frac{1}{a}= 2$,则$a^{2} + \frac{1}{a^{2}}$的值为()
A.2
B.4
C.6
D.8

答案： C

2.式子$2025 - a^{2} + 2ab - b^{2}$的最大值是()
A.2023
B.2024
C.2025
D.2026

答案： C

3.已知$n - m = 3$,则整式$n^{2} - m^{2} - 6m= $______．

答案： 9

4.如图,两个正方形的边长分别为$a和b$,如果$a + b = 10$,$ab = 20$,那么阴影部分的面积是______．

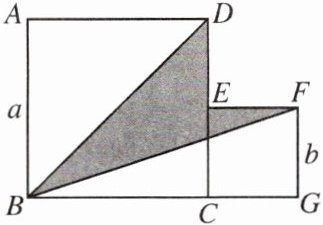
答案： 20

5.已知$x + y = - 10$,$xy = 16$,求下列各式的值．
(1)$x^{2} + y^{2}$；
(2)$x^{2} - xy + y^{2}$．

答案： 解:
(1)x²+y²=(x+y)²−2xy=(−10)²−2×16=68.
(2)x²−xy+y²=68−16=52.

6.阅读下列材料,解答相应问题：
数学知识伴随着人类文明的起源而产生,人类祖先为我们留下了许多珍贵的原始资料,如古巴比伦楔形文字泥板书．古巴比伦泥板上记载了两种利用平方数表计算两数乘积的公式：
$ab= \frac{1}{4}[(a + b)^{2} - (a - b)^{2}]…$①
$ab= \frac{1}{2}[(a + b)^{2} - a^{2}$______…$]$②
(1)补全材料中公式②中的空缺部分；
(2)验证材料中的公式①；
(3)当$a + b = 5$,$a - b = 7$时,利用公式①计算$ab$的值．

答案： 解:
(1)−b2
(2)公式①的右边=$\frac{1}{4}$[a²+b²+2ab−(a²+b²−2ab)]=
　$\frac{1}{4}$(a²+b²+2ab−a²−b²+2ab)=$\frac{1}{4}$×4ab=ab.因为公式①的左边=ab，所以公式①的左边=右边，公式成立.
(3)把a+b=5,a−b=7代入公式①,得ab=$\frac{1}{4}$×(5²−7²)=
　$\frac{1}{4}$×(−24)=−6.