《2025年时习之暑假衔接七年级数学北师大版》

简便运算：
(1)$(-2)^{101}×0.5^{100}$；
(2)$111^{2}-110×112$；
(3)$4+4×196+98^{2}$；
(4)$9\frac {5}{7}×(-10\frac {2}{7})$；
(5)$(3+1)(3^{2}+1)(3^{4}+1)(3^{8}+1)$．

答案： 解:
(1)原式=−2.　
(2)原式=1.　
(3)原式=10392.
(4)原式=−99$\frac{45}{49}$.　
(5)原式=$\frac{3^{16}−1}{2}$.

例 如图①,$AB= 7cm$,$AC⊥AB$,$BD⊥AB$,垂足分别为点A,B,$AC= 5cm$,点P在线段AB上以$2cm/s$的速度由点A向点B运动,同时点Q在射线BD上运动,它们运动的时间为$ts$．(当点P运动结束时,点Q运动随之结束)
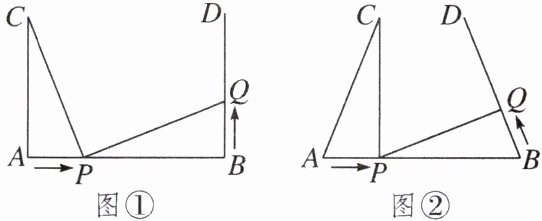
(1)若点Q的运动速度与点P的运动速度相等,当$t= 1$时,$\triangle ACP与\triangle BPQ$是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由；
(2)如图②,若“$AC⊥AB$,$BD⊥AB$”改为“$∠CAB= ∠DBA$”,点Q的运动速度为$xcm/s$,其他条件不变,当点P,Q运动到何处时有$\triangle ACP与\triangle BPQ$全等,则x的值为______．(直接写出x的值)

答案： 【解答】
(1)$\triangle ACP≌\triangle BPQ$,$PC⊥PQ$．理由如下：$\because AC⊥AB$,$BD⊥AB$,$\therefore ∠A= ∠B= 90^{\circ }$．$\because AP= BQ= 2×1= 2$,$\therefore BP= 5$．$\therefore BP= AC$．在$\triangle ACP和\triangle BPQ$中,$\left\{\begin{array}{l} AP= BQ,\\ ∠A= ∠B,\\ AC= BP,\end{array}\right. $$\therefore \triangle ACP≌\triangle BPQ(SAS)$．$\therefore ∠C= ∠BPQ$．$\because ∠C+∠APC= 90^{\circ }$,$\therefore ∠BPQ+∠APC= 90^{\circ }$．$\therefore ∠CPQ= 90^{\circ }$．$\therefore PC⊥PQ$．
(2)2或$\frac {20}{7}$