《2025年时习之暑假衔接七年级数学北师大版》

例2 飞机在空中水平飞行,某一时刻刚好飞到李想头顶上方4000米处,过了30秒,飞机距离李想头顶5000米.飞机每小时飞行多少千米？

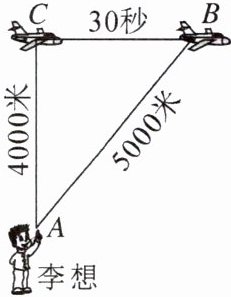
答案： 【解答】由勾股定理,可以得到$AB^2= BC^2+AC^2$,也就是$5000^2= BC^2+4000^2$,所以$BC= 3000$.飞机30秒飞行3000米,那么它1小时飞行的距离为$3000×60×60÷30= 360000$(米),即它飞行的速度为360千米/时.

2. 数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端A的绳子沿旗杆垂到地面时,测得多出部分BC的长为3m(如图①),再将绳子拉直(如图②),测得绳子末端的位置D到旗杆底部B的距离为9m,求旗杆AB的长.

答案： 解:设旗杆AB的长为x m，则AD=(x+3)m。又BD=9m，AB⊥BD，由勾股定理，得$(x+3)^{2}=x^{2}+9^{2}$。所以x=12，即旗杆AB的长为12m。

1. 王大爷离家出门散步,他先向正北走了60m,接着又向正东走了80m,此时他离家的距离为()
A. 70m
B. 80m
C. 90m
D. 100m

答案： D

2. 如图,一根竹子高9尺,折断后竹子顶端落在离竹子底端3尺处,折断处离地面的高度是()

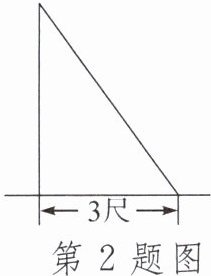
A. 3尺
B. 4尺
C. 5尺
D. 6尺

答案： B

3. 如图,用四块直角边为a,b,斜边为c的直角三角形拼成一个正方形,求图形中央的小正方形的面积.不难找到：解法(1)小正方形的面积= ______；解法(2)小正方形的面积= ______；由解法(1)(2),可以得到a,b,c的关系为：______.

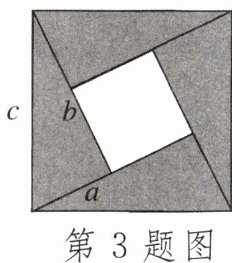
答案： $c^{2}-2ab$ $(b - a)^{2}$ $c^{2}=a^{2}+b^{2}$

4. 有一块边长为24米的正方形绿地,如图所示,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小明想在A处树立一个标牌“少走□米,踏之何忍”.请你计算后帮小明在标牌上的“□”填上适当的数字为______.

答案： 6

5. 如图,王大爷准备建一个蔬菜大棚,棚宽4m,高3m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积是______.

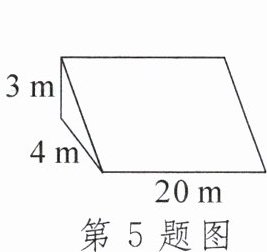
答案： 100m²　点拨:由图可知塑料薄膜的宽为5m，当阳光垂直照射塑料薄膜时透过面积最大。最大面积为20×5=100(m²)。

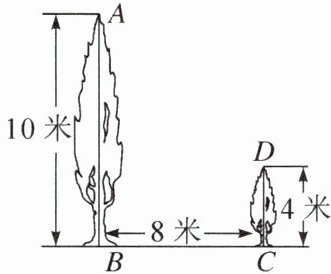
6. 如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行多少米？

答案：
解:如图，过点D作DE⊥AB于E，则依题意有AB=10米，BE=CD=4米，BC=8米，所以AE=AB - BE=6米。在Rt△AED中，由勾股定理得$AD^{2}=AE^{2}+ED^{2}=100$，所以AD=10米。所以小鸟至少飞行10米。