《2025年时习之暑假衔接七年级数学北师大版》

3.如图,已知$∠MBA+∠BAC+∠NCA= 360^{\circ }$．
(1)试说明：$MD// NE$；
(2)若$∠ABD= 70^{\circ }$,$∠ACE= 36^{\circ }$,$BP和CP分别平分∠ABD$,$∠ACE$,求$∠BPC$的度数．

答案： 3.解:
(1)过A向左作$AQ// MD$，所以$∠MBA+∠BAQ=180^{\circ}$。因为$∠MBA+∠BAC+∠NCA=360^{\circ}$，所以$∠QAC+∠NCA=180^{\circ}$。所以$AQ// NE$。所以$MD// NE$。
(2)过点P向左作$PF// MD$。因为$MD// NE$，所以$PF// NE$。所以$∠DBP=∠BPF$，$∠PCE=∠CPF$。因为$∠ABD=70^{\circ}$，$∠ACE=36^{\circ}$，BP平分$∠ABD$，CP平分$∠ACE$，所以$∠DBP=\frac{1}{2}∠ABD=35^{\circ}$，$∠PCE=\frac{1}{2}∠ACE=18^{\circ}$。所以$∠BPC=∠DBP+∠PCE=35^{\circ}+18^{\circ}=53^{\circ}$。

核心考点2：平行线中多拐点问题
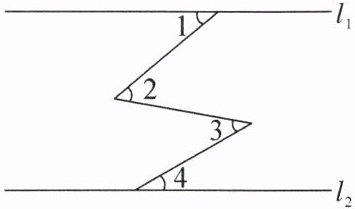
4.如图,直线$l_{1}// l_{2}$,若$∠1= 40^{\circ }$,$∠2比∠3大10^{\circ }$,则$∠4$的度数为____．

答案： 4.$30^{\circ}$

5.猜想说理：
(1)如图,$AB// CD// EF$,分别就图①、图②、图③写出$∠A$,$∠C$,$∠AFC$的关系,并任选其中一个图形说明理由．
拓展应用：
(2)如图④,若$AB// CD$,则$∠A+∠C+∠AFC= $____$^{\circ }$；
(3)在图⑤中,若$A_{1}B// A_{n}D$,请你用含$n的代数式表示∠1+∠2+∠3+∠4+... +∠n$的度数为____．

答案： 5.解:
(1)图①：$∠A+∠C=∠AFC$；图②：$∠A - ∠C=∠AFC$；图③：$∠C - ∠A=∠AFC$。
选图①，说明理由如下：因为$AB// CD// EF$，所以$∠A=∠AFE$，$∠C=∠EFC$。所以$∠A+∠C=∠AFE+∠EFC$，即$∠A+∠C=∠AFC$(答案不唯一)。
(2)360　
(3)$(n - 1)×180^{\circ}$

核心考点3：平行线在实际生活中的应用
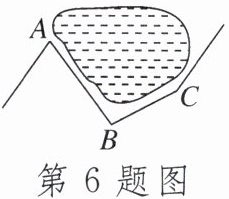
6.如图,一条公路修到湖边时,需绕湖而过,如果第一次拐弯处$∠A是72^{\circ }$,第三次拐弯处的$∠C是153^{\circ }$,这时道路恰好和第一次拐弯之前的道路平行,则$∠B$的度数为()

A.$81^{\circ }$
B.$99^{\circ }$
C.$108^{\circ }$
D.$120^{\circ }$

答案： 6.B

7.如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心$O的光线相交于点P$,点$F$为凸透镜右侧的焦点．若$∠1= 145^{\circ }$,$∠3= 60^{\circ }$,则$∠2$的度数为____．

答案： 7.$25^{\circ}$

8.如图①是一盏可以伸缩的台灯,它的优点是可以变化伸缩,找到合适的照明角度．图②是这盏台灯的示意图．已知台灯水平放置,当灯头$AB与支架CD$平行时可达到最佳照明角度,此时支架$BC与水平线BE的夹角∠CBE= 130^{\circ }$,两支架$BC和CD的夹角∠BCD= 110^{\circ }$．
(1)求此时支架$CD与底座MN的夹角∠CDM$的度数；
(2)求此时灯头$AB与水平线BE的夹角∠ABE$的度数．

答案：
8.解:
(1)如图，过点C作$CF// BE$，所以$∠BCF+∠CBE=180^{\circ}$。因为$∠CBE=130^{\circ}$，所以$∠BCF=50^{\circ}$。因为$∠BCD=110^{\circ}$，所以$∠DCF=∠BCD - ∠BCF=60^{\circ}$。因为$BE// MN$，所以$CF// MN$。

所以$∠CDM=∠DCF=60^{\circ}$。
(2)因为$AB// CD$，所以$∠ABC+∠BCD=180^{\circ}$。因为$∠BCD=110^{\circ}$，所以$∠ABC=70^{\circ}$。因为$∠CBE=130^{\circ}$，所以$∠ABE=∠CBE - ∠ABC=60^{\circ}$。