《2025年教材课本高中数学选择性必修第一册人教B版》

8.已知$AB$，$AC$，$AD$为长方体的三条棱，且$A(1,2,1)$，$B(1,5,1)$，$C(1,2,7)$，$D(3,2,1)$，求长方体这三条棱的长和体对角线的长.

答案： 易得$\overrightarrow{AB}=(0,3,0)$,$\overrightarrow{AC}=(0,0,6)$,$\overrightarrow{AD}=(2,0,0)$,
所以$|\overrightarrow{AB}|=\sqrt{0^{2}+3^{2}+0^{2}} = 3$,$|\overrightarrow{AC}|=\sqrt{0^{2}+0^{2}+6^{2}} = 6$,$|\overrightarrow{AD}|=\sqrt{2^{2}+0^{2}+0^{2}} = 2$.
体对角线的长度为$\sqrt{|\overrightarrow{AB}|^{2}+|\overrightarrow{AC}|^{2}+|\overrightarrow{AD}|^{2}}=\sqrt{3^{2}+6^{2}+2^{2}} = 7$.

9.任作一个平行六面体$ABCD - A'B'C'D'$，设$\overrightarrow{AB}=\boldsymbol{a}$，$\overrightarrow{AD}=\boldsymbol{b}$，$\overrightarrow{AA'}=\boldsymbol{c}$，分别作出向量$\overrightarrow{AM}$，使它等于如下向量:
　　　(1)$\boldsymbol{a}+\frac{1}{2}\boldsymbol{b}$;　　　　(2)$\frac{1}{2}\boldsymbol{a}+\frac{1}{2}\boldsymbol{b}+\frac{1}{2}\boldsymbol{c}$;　　　　(3)$\frac{1}{2}\boldsymbol{a}+\frac{1}{2}\boldsymbol{b}+\boldsymbol{c}$.

答案：
如图D2所示,$M_{1},M_{2},M_{3}$分别为$BC$,$AC'$,$B'D'$的中点.
(1)$\overrightarrow{AM_{1}}=a+\frac{1}{2}b$;
(2)$\overrightarrow{AM_{2}}=\frac{1}{2}a+\frac{1}{2}b+\frac{1}{2}c$;
(3)$\overrightarrow{AM_{3}}=\frac{1}{2}a+\frac{1}{2}b + c$.

1.在空间四边形$ABCD$中，连接$AC$，$BD$，设$M$，$G$分别是$BC$，$CD$的中点，化简下列各向量表达式:
　　　(1)$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AD}$;　　　　　　　　(2)$\overrightarrow{AD}-\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$.

答案：
任意作一个空间四边形如图D3所示,并连接$AC$,$BD$,$AM$,$AG$,$MD$.
(1)$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{AD}=2\overrightarrow{AG}$.
(2)$\overrightarrow{AD}-\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})=\overrightarrow{AD}-\overrightarrow{AM}=\overrightarrow{MD}$.

2.已知$\boldsymbol{a}$，$\boldsymbol{b}$都是空间向量，且$\langle\boldsymbol{a},\boldsymbol{b}\rangle=\frac{\pi}{4}$，求$\langle2\boldsymbol{a},-3\boldsymbol{b}\rangle$.

答案： $\langle 2a,-3b\rangle=\pi-\frac{\pi}{4}=\frac{3\pi}{4}$.

3.已知向量$\boldsymbol{a}$，$\boldsymbol{b}$均为单位向量，且它们的夹角为$60^{\circ}$，求$|\boldsymbol{a}+3\boldsymbol{b}|$.

答案： $|a + 3b|=\sqrt{(a + 3b)^{2}}=\sqrt{a^{2}+6a\cdot b + 9b^{2}}=\sqrt{|a|^{2}+6|a||b|\cos\langle a,b\rangle+9|b|^{2}}=\sqrt{1^{2}+6×1×1×\cos60^{\circ}+9×1^{2}}=\sqrt{13}$.

4.如果$\boldsymbol{a}+2\boldsymbol{b}-3\boldsymbol{c}=x\boldsymbol{a}+y\boldsymbol{b}+z\boldsymbol{c}$，那么一定有$x = 1$，$y = 2$，$z = -3$吗? 为什么?

答案： 不一定. 如当$a,b,c$都为零向量时,$x,y,z$有无数种解(举出反例即可).

5.已知空间直角坐标系中，平行六面体$ABCD - A_{1}B_{1}C_{1}D_{1}$满足:$A(-2,1,3)$，$B(2,2,1)$，$C(3,4,2)$，$D(-1,3,4)$，且平行六面体的体对角线的交点为$M(1,1,1)$，求$A_{1}$，$B_{1}$，$C_{1}$，$D_{1}$的坐标.

答案： 因为$M$分别为$AC_{1}$,$BD_{1}$,$CA_{1}$,$DB_{1}$的中点,所以由中点坐标公式,得$A_{1}(-1,-2,0)$,$B_{1}(3,-1,-2)$,$C_{1}(4,1,-1)$,$D_{1}(0,0,1)$.

6.在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，点$M$，$N$分别是面对角线$A_{1}B$与$B_{1}D_{1}$的中点，若$\overrightarrow{DA}=\boldsymbol{a}$，$\overrightarrow{DC}=\boldsymbol{b}$，$\overrightarrow{DD_{1}}=\boldsymbol{c}$，将$\overrightarrow{MN}$用向量$\boldsymbol{a}$，$\boldsymbol{b}$，$\boldsymbol{c}$表示出来.

答案： 依题意可得,$\overrightarrow{MN}=\overrightarrow{DN}-\overrightarrow{DM}=(\overrightarrow{DD_{1}}+\overrightarrow{D_{1}N})-(\overrightarrow{DA}+\overrightarrow{AM})=(c+\frac{1}{2}a+\frac{1}{2}b)-(a+\frac{1}{2}b+\frac{1}{2}c)=\frac{1}{2}c-\frac{1}{2}a$.

7.已知$\boldsymbol{a}$，$\boldsymbol{b}$是非零空间向量，根据下列各条件分别求$\langle\boldsymbol{a},\boldsymbol{b}\rangle$:
　　　(1)$\boldsymbol{a}\cdot\boldsymbol{b}=-|\boldsymbol{a}||\boldsymbol{b}|$;　　　　　　　　(2)$|\boldsymbol{a}|=|\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}|$;
　　　(3)$|\boldsymbol{a}|=|\boldsymbol{b}|=|\boldsymbol{a}+\boldsymbol{b}|$;　　　　　　(4)$|\boldsymbol{a}+\boldsymbol{b}|=|\boldsymbol{a}-\boldsymbol{b}|$.

答案：
(1)$\because a\cdot b=|a||b|\cos\langle a,b\rangle=-|a||b|$,
$\therefore\cos\langle a,b\rangle=-1$,即$\langle a,b\rangle = 180^{\circ}$.
(2)$|a - b|=\sqrt{(a - b)^{2}}=\sqrt{|a|^{2}-2|a||b|\cos\langle a,b\rangle+|b|^{2}}$,
$\because|a|=|b|=|a - b|$,
$\therefore|a|^{2}=|a|^{2}-2|a||a|\cos\langle a,b\rangle+|a|^{2}$,
$\therefore\cos\langle a,b\rangle=\frac{1}{2}$,$\therefore\langle a,b\rangle = 60^{\circ}$.
(3)$\because|a|=|b|=|a + b|$,$\therefore|a|^{2}=|a + b|^{2}$,
即$|a|^{2}=|a|^{2}+2|a||b|\cos\langle a,b\rangle+|b|^{2}$,
$\therefore|a|^{2}=|a|^{2}+2|a|^{2}\cos\langle a,b\rangle+|a|^{2}$,
$\therefore\cos\langle a,b\rangle=-\frac{1}{2}$,$\therefore\langle a,b\rangle = 120^{\circ}$.
(4)易知$|a + b|^{2}=|a - b|^{2}$,即$a^{2}+2a\cdot b + b^{2}=a^{2}-2a\cdot b + b^{2}$,
$\therefore 4a\cdot b = 0$,$\therefore\langle a,b\rangle = 90^{\circ}$.

8.已知$\{\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}\}$为单位正交基底，且非零向量$\boldsymbol{a}$的坐标为$(a_{1},a_{2},a_{3})$.
　　　(1)求证:$\boldsymbol{a}\cdot\boldsymbol{i}=a_{1}$，$\boldsymbol{a}\cdot\boldsymbol{j}=a_{2}$，$\boldsymbol{a}\cdot\boldsymbol{k}=a_{3}$;
　　　(2)分别求$\boldsymbol{a}$与基向量$\boldsymbol{i}$，$\boldsymbol{j}$，$\boldsymbol{k}$夹角的余弦.

答案：
(1)$\because\{i,j,k\}$为单位正交基底,
$\therefore i=(1,0,0)$,$j=(0,1,0)$,$k=(0,0,1)$.
$\therefore a\cdot i=(a_{1},a_{2},a_{3})\cdot(1,0,0)=a_{1}$,
$a\cdot j=(a_{1},a_{2},a_{3})\cdot(0,1,0)=a_{2}$,
$a\cdot k=(a_{1},a_{2},a_{3})\cdot(0,0,1)=a_{3}$.
(2)$\cos\langle a,i\rangle=\frac{a\cdot i}{|a||i|}=\frac{a_{1}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}}=\frac{a_{1}\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}}{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}$,
$\cos\langle a,j\rangle=\frac{a\cdot j}{|a||j|}=\frac{a_{2}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}}=\frac{a_{2}\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}}{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}$,
$\cos\langle a,k\rangle=\frac{a\cdot k}{|a||k|}=\frac{a_{3}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}}=\frac{a_{3}\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}}{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}$.

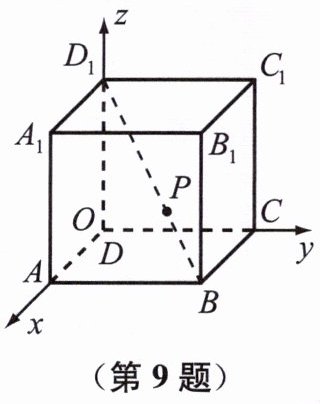
9.已知正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$的棱长为1，$P$为$BD_{1}$上一点，且$BP=\frac{1}{3}BD_{1}$.建立如图所示的空间直角坐标系，求点$P$的坐标.
　　　　　　　　　　　　　　　　　　　　　　　　　

答案： 连接$OP$,$OB$,根据题意知,$B(1,1,0)$,$D_{1}=(0,0,1)$,
$\therefore\overrightarrow{BD_{1}}=(-1,-1,1)$,$\therefore\overrightarrow{BP}=\frac{1}{3}\overrightarrow{BD_{1}}=(-\frac{1}{3},-\frac{1}{3},\frac{1}{3})$,
$\therefore\overrightarrow{OP}=\overrightarrow{OB}+\overrightarrow{BP}=(1,1,0)+(-\frac{1}{3},-\frac{1}{3},\frac{1}{3})=(\frac{2}{3},\frac{2}{3},\frac{1}{3})$,
$\therefore$点$P$的坐标为$(\frac{2}{3},\frac{2}{3},\frac{1}{3})$.