第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
13(10分)如图,在△ABC中,∠B = 30°,外角∠ACD = 100°,CE平分∠ACD,AF//CE交BC于点F,试求∠BAF的度数.


答案:
解:
∵∠ACD 为△ABC 的外角,
∴∠ACD = ∠B + ∠BAC,
∴∠BAC = ∠ACD - ∠B = 100° - 30° = 70°。
∵∠ACD = 100°,CE 平分∠ACD,
∴∠ACE = 1/2∠ACD = 1/2×100° = 50°。
∵AF//CE,
∴∠CAF = ∠ACE = 50°,
∴∠BAF = ∠BAC - ∠CAF = 70° - 50° = 20°。
∵∠ACD 为△ABC 的外角,
∴∠ACD = ∠B + ∠BAC,
∴∠BAC = ∠ACD - ∠B = 100° - 30° = 70°。
∵∠ACD = 100°,CE 平分∠ACD,
∴∠ACE = 1/2∠ACD = 1/2×100° = 50°。
∵AF//CE,
∴∠CAF = ∠ACE = 50°,
∴∠BAF = ∠BAC - ∠CAF = 70° - 50° = 20°。
14(12分)(安徽合肥期末)按要求完成下列各小题.
(1)一个多边形的内角和比它的外角和多900°,求这个多边形的边数;
(2)如图,若正五边形ABCDE和长方形AFCG按如图方式叠放在一起,求∠EAF的度数.

(1)一个多边形的内角和比它的外角和多900°,求这个多边形的边数;
(2)如图,若正五边形ABCDE和长方形AFCG按如图方式叠放在一起,求∠EAF的度数.

答案:
解:
(1)设这个多边形的边数为 n,根据题意,得(n - 2)×180° = 360° + 900°,解得 n = 9,故这个多边形的边数是 9。
(2)
∵正五边形内角和为(5 - 2)×180° = 540°,
∴其每个内角为 540°÷5 = 108°。
∵长方形每个内角为 90°,
∴∠F = 90°,
∴∠BAF = ∠ABC - ∠F = 108° - 90° = 18°,
∴∠EAF = ∠EAB + ∠BAF = 108° + 18° = 126°。
(1)设这个多边形的边数为 n,根据题意,得(n - 2)×180° = 360° + 900°,解得 n = 9,故这个多边形的边数是 9。
(2)
∵正五边形内角和为(5 - 2)×180° = 540°,
∴其每个内角为 540°÷5 = 108°。
∵长方形每个内角为 90°,
∴∠F = 90°,
∴∠BAF = ∠ABC - ∠F = 108° - 90° = 18°,
∴∠EAF = ∠EAB + ∠BAF = 108° + 18° = 126°。
15(14分)(河南鹤壁期末)如图所示,AD为△ABC的高,AE、BF为△ABC的角平分线,若∠CBF = 30°,∠AFB = 70°.
(1)求∠DAE的度数;
(2)若点M为线段BC上任意一点,当△MFC为直角三角形时,直接写出∠BFM的度数.

(1)求∠DAE的度数;
(2)若点M为线段BC上任意一点,当△MFC为直角三角形时,直接写出∠BFM的度数.

答案:
解:
(1)
∵BF 为△ABC 的角平分线,∠CBF = 30°,
∴∠ABF = ∠CBF = 30°,∠ABC = 2∠CBF = 60°。
∵AD 为△ABC 的高,
∴∠ADB = 90°,
∴∠BAD = 30°。在△ABF 中,∠ABF = 30°,∠AFB = 70°,
∴∠BAF = 80°。
∵AE 为△ABC 的角平分线,
∴∠BAE = 40°,
∴∠DAE = ∠BAE - ∠BAD = 10°。
(2)
∵∠ABC = 60°,∠BAC = 80°,
∴∠C = 180° - ∠ABC - ∠BAC = 40°,①当∠CFM = 90°时,∠BFC = 180° - ∠AFB = 110°,
∵∠CFM = 90°,
∴∠BFM = ∠BFC - ∠CFM = 20°;②当∠CMF = 90°时,∠BFM = ∠CMF - ∠CBF = 60°。综上,∠BFM 的度数为 20°或 60°。 解题关键点:求角的度数时,可以把未知角放在三角形中,利用三角形内角和定理求解,也可以利用外角的性质把未知角转化为已知角的和或差求解。
(1)
∵BF 为△ABC 的角平分线,∠CBF = 30°,
∴∠ABF = ∠CBF = 30°,∠ABC = 2∠CBF = 60°。
∵AD 为△ABC 的高,
∴∠ADB = 90°,
∴∠BAD = 30°。在△ABF 中,∠ABF = 30°,∠AFB = 70°,
∴∠BAF = 80°。
∵AE 为△ABC 的角平分线,
∴∠BAE = 40°,
∴∠DAE = ∠BAE - ∠BAD = 10°。
(2)
∵∠ABC = 60°,∠BAC = 80°,
∴∠C = 180° - ∠ABC - ∠BAC = 40°,①当∠CFM = 90°时,∠BFC = 180° - ∠AFB = 110°,
∵∠CFM = 90°,
∴∠BFM = ∠BFC - ∠CFM = 20°;②当∠CMF = 90°时,∠BFM = ∠CMF - ∠CBF = 60°。综上,∠BFM 的度数为 20°或 60°。 解题关键点:求角的度数时,可以把未知角放在三角形中,利用三角形内角和定理求解,也可以利用外角的性质把未知角转化为已知角的和或差求解。
16(16分)【新趋势·探究性问题】如图,在四边形ABCD中,∠B + ∠D = 180°,∠DCE是四边形ABCD的一个外角.
(1)如图1,试判断∠DCE与∠A的数量关系,并说明理由;
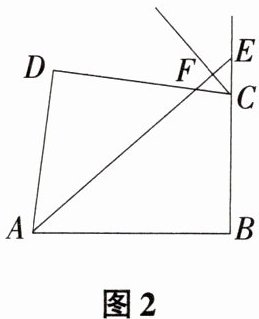
(2)如图2,若∠B = 90°,AE平分∠BAD,CF平分∠DCE,且AE与CF相交于点F,试判断AE与CF的位置关系,并说明理由.
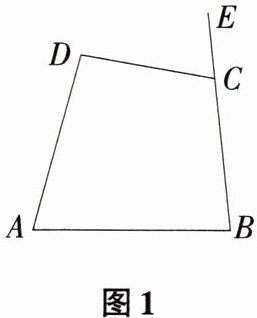
(1)如图1,试判断∠DCE与∠A的数量关系,并说明理由;
(2)如图2,若∠B = 90°,AE平分∠BAD,CF平分∠DCE,且AE与CF相交于点F,试判断AE与CF的位置关系,并说明理由.


答案:
解:
(1)∠DCE = ∠A。理由如下:
∵∠B + ∠D = 180°,四边形 ABCD 的内角和为 360°,
∴∠A + ∠DCB = 360° - 180° = 180°。
∵∠DCE + ∠DCB = 180°,
∴∠DCE = ∠A。
(2)AE⊥CF。理由如下:如图,设 AE 与 CD 交于点 G。 ![img id=4] 由
(1)可知,∠BAD = ∠DCE,
∵AE 平分∠BAD,CF 平分∠DCE,
∴∠DAG = ∠BAG = ∠GCF = ∠ECF。又
∵∠DGA = ∠FGC,
∴∠ADG = ∠CFG。
∵∠B + ∠D = 180°,∠B = 90°,
∴∠ADG = 90°,
∴∠CFG = 90°,即 AE⊥CF。
(1)∠DCE = ∠A。理由如下:
∵∠B + ∠D = 180°,四边形 ABCD 的内角和为 360°,
∴∠A + ∠DCB = 360° - 180° = 180°。
∵∠DCE + ∠DCB = 180°,
∴∠DCE = ∠A。
(2)AE⊥CF。理由如下:如图,设 AE 与 CD 交于点 G。 ![img id=4] 由
(1)可知,∠BAD = ∠DCE,
∵AE 平分∠BAD,CF 平分∠DCE,
∴∠DAG = ∠BAG = ∠GCF = ∠ECF。又
∵∠DGA = ∠FGC,
∴∠ADG = ∠CFG。
∵∠B + ∠D = 180°,∠B = 90°,
∴∠ADG = 90°,
∴∠CFG = 90°,即 AE⊥CF。
查看更多完整答案,请扫码查看


