《2025年初中学霸创新题七年级数学下册华师大版》

10（易错题）一个多边形截去一个角后，形成的另一个多边形的内角和为720°，那么原多边形的边数为 （ ）
A. 5
B. 5或6
C. 6或7
D. 5或6或7

答案： D

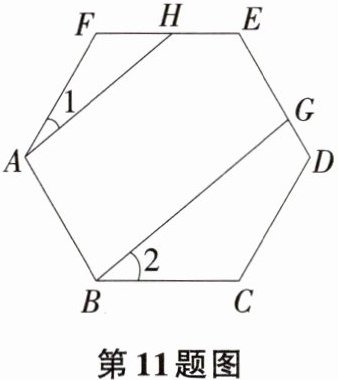
11 如图，已知正六边形ABCDEF，点G、H分别是DE、EF上一点，且AH//BG，若∠1=20°，则∠2的度数为 （ ）

A. 50°
B. 45°
C. 40°
D. 35°

答案： C

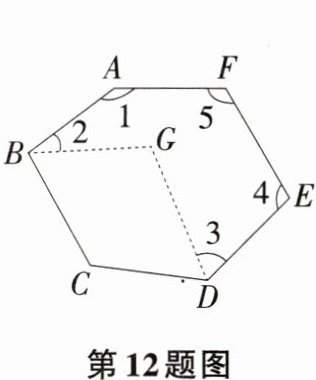
12 如图，将六边形纸片ABCDEF沿虚线剪去一个角（∠BCD）后，得到∠1+∠2+∠3+∠4+∠5=470°，则六边形ABCDEF的内角和为_______，∠BGD的度数为_______.

答案： 720°@@110°

13（河南周口太康阶段练习）一个多边形除一个内角外，其余各内角之和是2 570°，则这个内角是_______°.

答案： 130

14（一题多解）某实验中学七年级的6个班举行拔河比赛，比赛采用单循环积分制（即每两个班都要进行一场比赛），你能算出一共需要进行多少场比赛吗？

答案： 解：解法一：如图，将七年级的6个班看成六边形的6个顶点，由多边形的对角线公式可得六边形的对角线条数为$\frac{6×(6 - 3)}{2}$ = 9，故共比赛9 + 6 = 15（场）. 解法二：6个班进行单循环赛，则每个班与其他5个班要进行5场比赛，6个班共进行6×5 = 30（场），但每场比赛重复计算了一次，所以共比赛30÷2 = 15（场）. 答：一共需要进行15场比赛.

15【新趋势·探究性问题】在一个多边形中，一个内角相邻的外角与其他各内角的和为600°.
（1）如果这个多边形是五边形，请求出这个外角的度数；
（2）是否存在符合题意的其他多边形？如果存在，请求出这个多边形的边数及这个外角的度数；如果不存在，请说明理由.

答案： 解：
(1)设这个外角的度数是x，则(5 - 2)×180° - (180° - x) + x = 600°，解得x = 120°，故这个外角的度数是120°.
(2)存在. 理由如下： 设这个多边形的边数是n，这个外角的度数是y，则(n - 2)×180° - (180° - y) + y = 600°，整理得y = 570° - 90°n.
∵0° y 180°，即0° 570° - 90°n 180°，解得4$\frac{1}{3}$ n 6$\frac{1}{3}$，且n为正整数，
∴n = 5或n = 6. 故存在符合题意的其他多边形，这个多边形的边数是6，这个外角的度数为570° - 90°×6 = 30°.

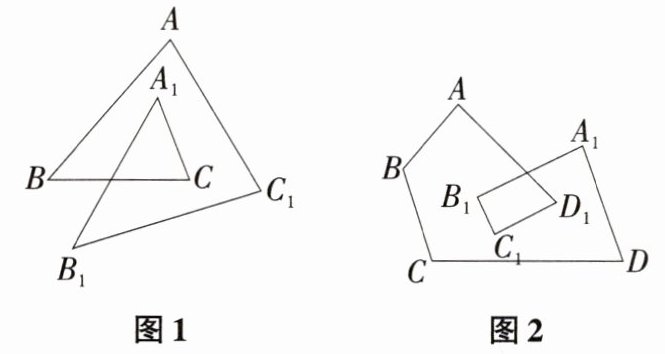
16【新趋势·规律探究题】如图，把图1称为二环三角形，它的内角和∠A+∠B+∠C+∠A₁+∠B₁+∠C₁=_______°；把图2称为二环四边形，它的内角和∠A+∠B+∠C+∠D+∠A₁+∠B₁+∠C₁+∠D₁=_______°；…；依此规律，请你探究二环n边形的内角和是多少度？(用含n的式子表示）

答案： 360@@720