《2025年初中学霸创新题七年级数学下册华师大版》

1（河南周口太康期中）下列各式中：①$x＞0$；②$x =3$；③$3＜4$；④$x + 2\leqslant3$；⑤$4x + 1$，其中不等式的个数为 ( )
A. 1
B. 2
C. 3
D. 4

答案： C@@解析：①$x ＞ 0$，③$3 4$，④$x + 2\leq3$是不等式；②$x = 3$是等式，⑤$4x + 1$是代数式，故不等式的个数为3. 故选C. 解题关键点：判断一个式子是否为不等式，关键看所给的式子是否含不等号.

2（教材P59练习第2题改编）在$4、3、2、1、0、-\frac{3}{2}、-\frac{10}{3}$中，能使不等式$3x - 2＞2x$成立的数有( )
A. 1个
B. 2个
C. 3个
D. 4个

答案： B@@解析：将题中所给的7个数分别代入不等式$3x - 2＞2x$中，只有4、3能使不等式成立. 故选B. 解题关键点：判断一个数是否为不等式的解，只需将这个数代替不等式中的未知数，看不等式是否成立. 若成立，则该数是不等式的解，否则不是.

3【新趋势·开放性问题】请写出一个关于$x$的不等式，使$-2、3$都是它的解：_________.

答案： $x\geq - 2$(答案不唯一)

4（河南南阳新野期中）一次知识竞赛共有20道选择题，答对一题得5分；答错或不答，每题扣1分. 要使总得分不少于88分，则至少要答对几道题？若设答对$x$道题，可列出的不等式为 ( )
A. $5x-(20 - x)＞88$
B. $5x-(20 - x)＜88$
C. $5x-(20 - x)\leqslant88$
D. $5x-(20 - x)\geqslant88$

答案： D@@解析：答对$x$道题，则答错或不答$(20 - x)$道题，根据题意，可列不等式$5x-(20 - x)\geq88$. 故选D.

5（易错题）用不等式表示下面的关系：
(1)$b$的2倍小于2；(2)$2x$与$3y$的差是非负数；
(3)$m$与$n$的和的2倍不大于5.

答案： 解：
(1)$2b 2$.
(2)$2x - 3y\geq0$.
(3)$2(m + n)\leq5$. 易错点：本题易因忽略“非”“不”而不能正确理解关键词语“非负数”“不大于”等文字的意义，从而不能正确地用符号表示不等关系致错.

6【新定义·新运算问题】定义：对于任意有理数$a$，用$＜a＞$表示大于$a$的最小整数，例如：$＜2.5＞=3$，$＜4＞=5$，$＜-1.5＞=-1$. 若$＜a＞=-3$，则$a$的取值范围是 ( )
A. $-4＜a\leqslant-3$
B. $-4＜a＜-3$
C. $-4\leqslant a\leqslant-3$
D. $-4\leqslant a＜-3$

答案： D@@解析：根据$a＞$表示大于$a$的最小整数，可得当$a＞ = - 3$时，$a$的取值范围是$-4\leq a - 3$. 故选D.

7 为了加强对校内外的安全监控，创建“平安校园”. 某学校计划增加15台监控摄像设备，现有甲、乙两种型号的设备，其中价格、有效监控半径如表所示：

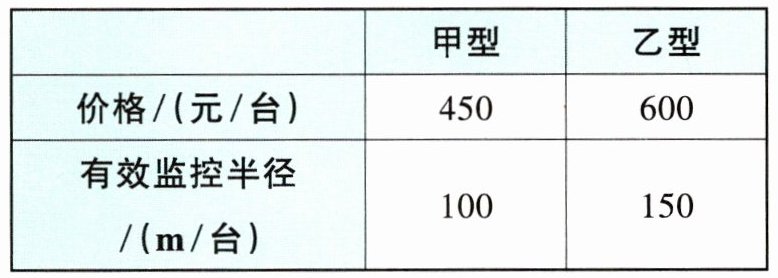
(1)若购买该批设备的资金不超过7 200元，请你写出购买的甲型设备数量$x$(台)应满足的不等式；
(2)若要求有效监控半径覆盖范围大于1 600 m，请你写出购买的甲型设备数量$x$(台)应满足的不等式.

答案： 解：
(1)购买甲型设备$x$台，则购买乙型设备$(15 - x)$台，根据题意，得$450x + 600(15 - x)\leq7200$.
(2)购买甲型设备$x$台，则购买乙型设备$(15 - x)$台，根据题意，得$100x + 150(15 - x)＞1600$.