第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
9(四川凉山州中考)一副直角三角板按如图所示的方式摆放,点E在AB的延长线上,当DF//AB时,∠EDB的度数为 ( )
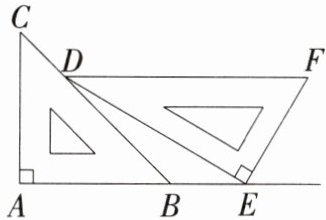
A. 10°
B. 15°
C. 30°
D. 45°

A. 10°
B. 15°
C. 30°
D. 45°
答案:
B
10如图所示,∠A=15°,∠ABC=90°,∠ACB=∠DCE,∠ADC=∠EDF,∠CED=∠FEG,则∠F的度数等于 ( )
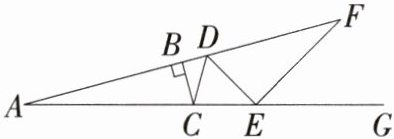
A. 40°
B. 35°
C. 30°
D. 25°

A. 40°
B. 35°
C. 30°
D. 25°
答案:
C
11(河南南阳桐柏期中)一个等边三角形、一个直角三角形以及一个等腰三角形如图放置,等腰三角形的底角∠3=80°,则∠1+∠2=______.
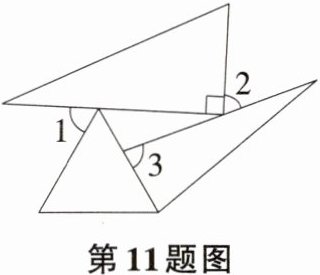

答案:
130°
12【新趋势·规律探究题】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A₁,得∠A₁;∠A₁BC和∠A₁CD的平分线交于点A₂,得∠A₂;…;∠A₂₀₂₄BC和∠A₂₀₂₄CD的平分线交于点A₂₀₂₅,则∠A₂₀₂₅=______°.
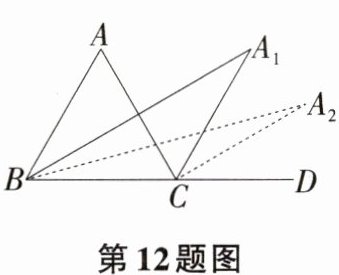

答案:
($\frac{m}{2^{2025}}$)
13(河南开封龙亭校级期末)如图,△ABC的外角∠ACD的平分线与线段BA的延长线交于点F,点E在线段CF上,且∠AEF+∠FCD=180°.
(1)试说明:AE//BC;
(2)若∠B=28°,∠ACF=62°,求∠BAC的度数.
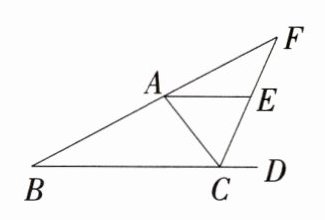
(1)试说明:AE//BC;
(2)若∠B=28°,∠ACF=62°,求∠BAC的度数.

答案:
解:
(1)
∵∠AEF + ∠AEC = 180°,∠AEF + ∠FCD = 180°,
∴∠AEC = ∠FCD,
∴AE//BC。
(2)
∵CF是∠ACD的平分线,∠ACF = 62°,∠B = 28°,
∴∠ACD = 2∠ACF = 124°,
∴∠BAC = ∠ACD - ∠B = 124° - 28° = 96°。
(1)
∵∠AEF + ∠AEC = 180°,∠AEF + ∠FCD = 180°,
∴∠AEC = ∠FCD,
∴AE//BC。
(2)
∵CF是∠ACD的平分线,∠ACF = 62°,∠B = 28°,
∴∠ACD = 2∠ACF = 124°,
∴∠BAC = ∠ACD - ∠B = 124° - 28° = 96°。
14【新趋势·探究性问题】小明在学习中遇到这样一个问题:如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E,猜想∠B、∠ACB、∠E的数量关系.
(1)小明阅读题目后,没有发现数量关系与解题思路,于是尝试从具体的情况开始探索,若∠B=35°,∠ACB=85°,则∠E=______;
(2)小明继续探究,设∠B=α,∠ACB=β(β>α),当点P在线段AD上运动时,求∠E的大小.(用含α、β的代数式表示)
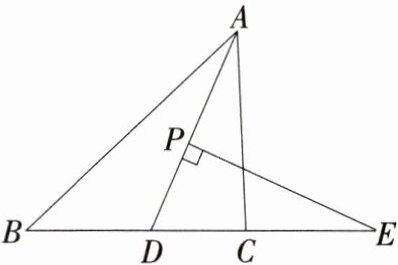
(1)小明阅读题目后,没有发现数量关系与解题思路,于是尝试从具体的情况开始探索,若∠B=35°,∠ACB=85°,则∠E=______;
(2)小明继续探究,设∠B=α,∠ACB=β(β>α),当点P在线段AD上运动时,求∠E的大小.(用含α、β的代数式表示)

答案:
25°@@解:
(2)
∵AD平分∠BAC,
∴∠BAD = ∠CAD = $\frac{1}{2}$∠BAC。
∵∠B + ∠ACB + ∠BAC = 180°,∠B = α,∠ACB = β,
∴∠BAC = 180° - α - β,
∴∠BAD = $\frac{1}{2}$(180° - α - β),
∴∠PDE = ∠B + ∠BAD = α + $\frac{1}{2}$(180° - α - β) = 90° + $\frac{1}{2}$(α - β)。
∵PE⊥AD,
∴∠PDE + ∠E = 90°,
∴∠E = 90° - ∠PDE = 90° - [90° + $\frac{1}{2}$(α - β)] = $\frac{1}{2}$(β - α)。 核心素养:本题考查了数学核心素养中的几何直观和推理能力,利用三角形内角和及外角的性质表示出所求角是解题关键。
(2)
∵AD平分∠BAC,
∴∠BAD = ∠CAD = $\frac{1}{2}$∠BAC。
∵∠B + ∠ACB + ∠BAC = 180°,∠B = α,∠ACB = β,
∴∠BAC = 180° - α - β,
∴∠BAD = $\frac{1}{2}$(180° - α - β),
∴∠PDE = ∠B + ∠BAD = α + $\frac{1}{2}$(180° - α - β) = 90° + $\frac{1}{2}$(α - β)。
∵PE⊥AD,
∴∠PDE + ∠E = 90°,
∴∠E = 90° - ∠PDE = 90° - [90° + $\frac{1}{2}$(α - β)] = $\frac{1}{2}$(β - α)。 核心素养:本题考查了数学核心素养中的几何直观和推理能力,利用三角形内角和及外角的性质表示出所求角是解题关键。
查看更多完整答案,请扫码查看


