《2025年初中学霸创新题七年级数学下册华师大版》

10（吉林长春德惠期中）如果方程组$\begin{cases}x + y = ★,\\2x + y = 16\end{cases}$的解为$\begin{cases}x = 6,\\y = ■,\end{cases}$那么被“★、■”遮住的两个数分别为 ( )
A. 3、10
B. 4、10
C. 10、4
D. 10、3

答案： C

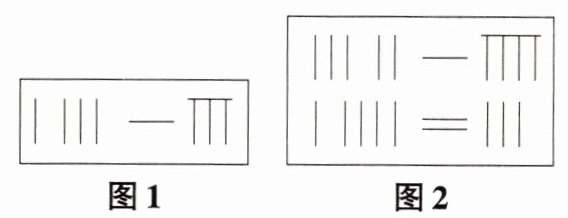
11【新情境·数学文化】“方程”二字最早见于我国《九章算术》这部数学经典著作中，该书“方程”一章中介绍了一种用“算筹图”解决一次方程组的方法. 如图1，从左向右的符号中，前两个符号分别代表未知数$x、y$的系数，因此，根据此图可以列出方程$x + 3y = 18$. 仔细分析图1所表示方程的例子，根据图2列出方程组为______________.

答案： $\begin{cases}3x + 2y = 19\\x + 4y = 23\end{cases}$

12（河南洛阳孟津期中）小明和小文解一个二元一次方程组$\begin{cases}cx - 3y = - 2,\\ax + by = 2,\end{cases}$小明正确解得$\begin{cases}x = 1,\\y = - 1,\end{cases}$小文因抄错了$c$，解得$\begin{cases}x = 2,\\y = - 6.\end{cases}$已知小文除抄错了$c$外，没有发生其他错误，则$a - 3b + c$的值为_______.

答案： -4

13【新趋势·阅读理解题】阅读下列材料，解答下面的问题:
我们知道方程$2x + 3y = 12$有无数组解，但在实际生活中我们往往只需求出其正整数解.
例：由$2x + 3y = 12$，得$y=\frac{12 - 2x}{3}$. 根据$x、y$为正整数，运用尝试法可以知道方程$2x + 3y = 12$的正整数解为$\begin{cases}x = 3,\\y = 2.\end{cases}$
问题：
(1)请你直接写出方程$3x - y = 6$的一组正整数解___________；
(2)若$\frac{12}{x - 3}$为自然数，求满足条件的正整数$x$的值；
(3)七年级某班为了奖励学生学习的进步，购买单价为3元的笔记本与单价为5元的钢笔两种奖品，共花费48元，问有哪几种购买方案?

答案： 解： - （1）$\begin{cases}x = 3\\y = 3\end{cases}$（答案不唯一） 提示：由方程$3x - y = 6$得$y = 3x - 6$，当$x = 3$时，$y = 3×3 - 6 = 3$. - （2）$\because\frac{12}{x - 3}$为自然数，$\therefore12$能被$x - 3$整除，$\therefore x - 3 = 1$或$x - 3 = 2$或$x - 3 = 3$或$x - 3 = 4$或$x - 3 = 6$或$x - 3 = 12$，解得$x = 4$或$x = 5$或$x = 6$或$x = 7$或$x = 9$或$x = 15$. - （3）设购买了$m$本笔记本，$n$支钢笔，根据题意，得$3m + 5n = 48$，即$m = 16-\frac{5}{3}n$.$\because m$、$n$为正整数，$\therefore$①$n = 3$时，$m = 11$；②$n = 6$时，$m = 6$；③$n = 9$时，$m = 1$. 答：有3种购买方案， 方案①：购买笔记本11本，钢笔3支； 方案②：购买笔记本6本，钢笔6支； 方案③：购买笔记本1本，钢笔9支.

1.（吉林长春朝阳期中）若$\begin{cases}x = - 1,\\y = 2\end{cases}$是二元一次方程$2y - ax = - 5$的一组解，则$a$的值为_______.

答案： -9

2. 若关于$x、y$的二元一次方程组$\begin{cases}x + y = 3,\\2x - ay = 5\end{cases}$的解是$\begin{cases}x = b,\\y = 1,\end{cases}$则$a^{b}$的值为_______.

答案： 1