《2025年初中学霸创新题七年级数学下册华师大版》

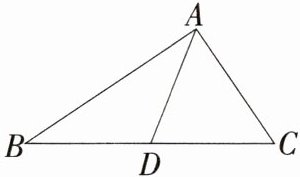
1如图，△ABC的周长为18，BC=8，AD是边BC上的中线，AD把△ABC分成的两个三角形的周长相差2，求AC的长度．

答案： 解：
∵△ABC的周长为18，BC = 8，
∴AB + AC = 18 - BC = 10。
∵AD是边BC上的中线，
∴BD = CD。
∵中线AD把△ABC分成的两个三角形的周长相差2，
∴分两种情况讨论： ①△ABD的周长比△ACD的周长大2，则(AB + BD + AD) - (AC + CD + AD) = AB - AC = 2。可列方程组$\begin{cases}AB + AC = 10\\AB - AC = 2\end{cases}$，解得$\begin{cases}AB = 6\\AC = 4\end{cases}$。 ②△ACD的周长比△ABD的周长大2，则(AC + CD + AD) - (AB + BD + AD) = AC - AB = 2。可列方程组$\begin{cases}AB + AC = 10\\AC - AB = 2\end{cases}$，解得$\begin{cases}AB = 4\\AC = 6\end{cases}$。 综上所述，AC的长度是4或6。

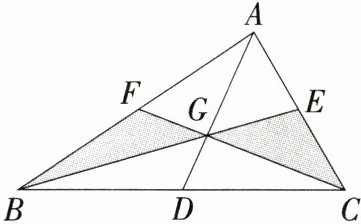
2（山东济南槐荫期末）如图，△ABC的三边的中线AD、BE、CF的公共点为G，且AG∶GD=2∶1，若S△ABC=12，求图中阴影部分的面积．

答案： 解：
∵AG:GD = 2:1，
∴AG:AD = 2:3，
∴$S_{\triangle ABG}$ = $\frac{2}{3}$$S_{\triangle ABD}$。
∵AD、BE、CF是△ABC三边的中线，
∴$S_{\triangle ABD}$ = $\frac{1}{2}$$S_{\triangle ABC}$，$S_{\triangle BCF}$ = $\frac{1}{2}$$S_{\triangle ABC}$，
∴$S_{\triangle ABG}$ = $\frac{2}{3}$×$\frac{1}{2}$$S_{\triangle ABC}$ = $\frac{1}{3}$$S_{\triangle ABC}$，
∴$S_{\triangle BGF}$ = $\frac{1}{2}$$S_{\triangle ABG}$ = $\frac{1}{6}$$S_{\triangle ABC}$ = $\frac{1}{6}$×12 = 2。同理$S_{\triangle CGE}$ = $\frac{1}{2}$$S_{\triangle ACG}$ = $\frac{1}{6}$$S_{\triangle ABC}$ = 2，所以$S_{阴影}$ = $S_{\triangle BGF}$ + $S_{\triangle CGE}$ = 2 + 2 = 4。 解题关键点：找出△BGF、△CGE与△ABC之间的关系是本题求解的关键。

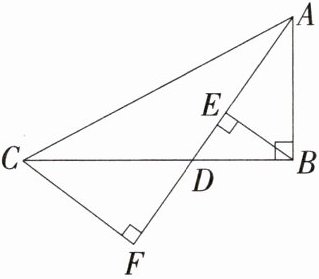
3【新趋势·动点探究题】如图，在直角三角形ABC中，∠ABC=90°，点D沿BC自B向C运动（点D与点B、C不重合），作BE⊥AD于点E，CF⊥AD于点F. 在点D的运动过程中，试判断BE+CF的值是否发生改变？

答案： 解：由$S_{\triangle ABC}$ = $S_{\triangle ABD}$ + $S_{\triangle ACD}$得，$S_{\triangle ABC}$ = $\frac{1}{2}$AD·BE + $\frac{1}{2}$AD·CF = $\frac{1}{2}$AD·(BE + CF)。因为点D沿BC自B向C运动，所以AD的长度逐渐增加。因为△ABC的面积不变，所以BE + CF的值逐渐减小。

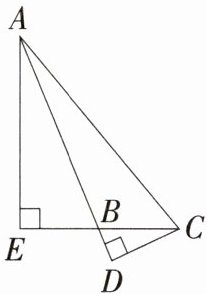
4（河南洛阳洛龙阶段练习）如图，AE⊥EC于点E，CD⊥AD于点D，AD交EC于点B. 若AB=5，BC=2，CD=$\frac{9}{5}$，求AE的长度．

答案： 解：
∵AE⊥EC，CD⊥AD，由三角形高的定义可知，△ABC的边BC上的高为AE，边AB上的高为CD，
∴$S_{\triangle ABC}$ = $\frac{1}{2}$BC·AE = $\frac{1}{2}$AB·CD，
∴$\frac{1}{2}$×2×AE = $\frac{1}{2}$×5×$\frac{9}{5}$，解得AE = $\frac{9}{2}$。

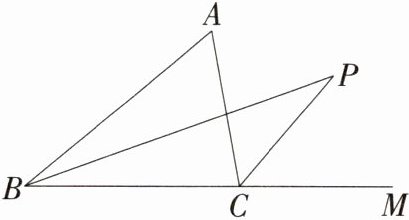
5（教材P93第6题改编）如图，BP是△ABC中∠ABC的平分线，CP是△ABC的外角∠ACM的平分线，如果∠ABP=20°，∠ACP=50°，求∠A+∠P的值．

答案： 解：
∵BP是△ABC中∠ABC的平分线，CP是△ABC的外角∠ACM的平分线，∠ABP = 20°，∠ACP = 50°，
∴∠CBP = ∠ABP = 20°，∠ABC = 2∠ABP = 40°，∠MCP = ∠ACP = 50°，∠ACM = 2∠ACP = 100°。
∵∠ACM = ∠ABC + ∠A，∠MCP = ∠CBP + ∠P，
∴∠A = ∠ACM - ∠ABC = 100° - 40° = 60°，∠P = ∠MCP - ∠CBP = 50° - 20° = 30°，
∴∠A + ∠P = 60° + 30° = 90°。