第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
9 如图,一个盛有水的圆柱形玻璃容器的内底面半径为10 cm,容器内水的高度为12 cm.把一根半径为2 cm的玻璃棒垂直插入水中,则容器内的水将升高_______cm.(假设水不会溢出)
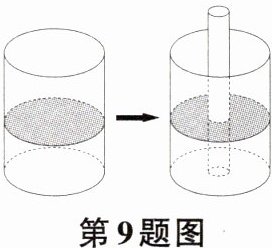

答案:
0.5
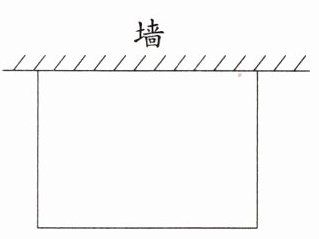
10(教材P20第1题改编)李师傅正在准备用篱笆修建一个长方形鸡舍栅栏,栅栏一面靠墙(墙面长度不限),三面用篱笆,篱笆总长60 m,篱笆围成的长方形鸡舍的长比宽多6 m,请你用所学的知识解决以下问题.(篱笆的占地面积忽略不计)
(1)如图,如果长方形鸡舍的长与墙为对面,长方形鸡舍的面积是多少?
(2)如果要在墙的对面留一个3 m宽的门(门不使用篱笆),那么长方形鸡舍的面积又是多少?
(1)如图,如果长方形鸡舍的长与墙为对面,长方形鸡舍的面积是多少?
(2)如果要在墙的对面留一个3 m宽的门(门不使用篱笆),那么长方形鸡舍的面积又是多少?

答案:
解:
(1)设鸡舍的宽为x m,则长为(x + 6)m,依题意,得x + (x + 6) + x = 60,解得x = 18,所以鸡舍的长为18 + 6 = 24(m),面积为18×24 = 432(m²). 答:长方形鸡舍的面积是432 m².
(2)设鸡舍的宽为y m,则鸡舍的长为(y + 6)m. 当鸡舍的长与墙为对面时,依题意,得y + y + (y + 6 - 3) = 60,解得y = 19,所以鸡舍的长为19 + 6 = 25(m). 鸡舍面积为19×25 = 475(m²). 当鸡舍的宽与墙为对面时,依题意,得2(y + 6) + y - 3 = 60,解得y = 17,所以鸡舍的长为17 + 6 = 23(m). 鸡舍面积为17×23 = 391(m²). 答:如果在墙对面留一个3 m宽的门,那么鸡舍面积为475 m²或391 m².
(1)设鸡舍的宽为x m,则长为(x + 6)m,依题意,得x + (x + 6) + x = 60,解得x = 18,所以鸡舍的长为18 + 6 = 24(m),面积为18×24 = 432(m²). 答:长方形鸡舍的面积是432 m².
(2)设鸡舍的宽为y m,则鸡舍的长为(y + 6)m. 当鸡舍的长与墙为对面时,依题意,得y + y + (y + 6 - 3) = 60,解得y = 19,所以鸡舍的长为19 + 6 = 25(m). 鸡舍面积为19×25 = 475(m²). 当鸡舍的宽与墙为对面时,依题意,得2(y + 6) + y - 3 = 60,解得y = 17,所以鸡舍的长为17 + 6 = 23(m). 鸡舍面积为17×23 = 391(m²). 答:如果在墙对面留一个3 m宽的门,那么鸡舍面积为475 m²或391 m².
11【新趋势·探究性问题】如图1是甲、乙两个圆柱形水槽轴截面图,甲槽内水位高度为12 cm,乙槽内无水,现将甲槽内的水注入乙槽.
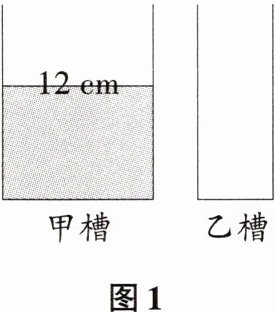
(1)若甲槽的底面积是乙槽的2倍.
①当甲槽内水位下降x cm,则乙槽水位上升_______cm;(用含x的代数式表示)
②当甲槽与乙槽水位高度相等时,求水槽中水位的高度;
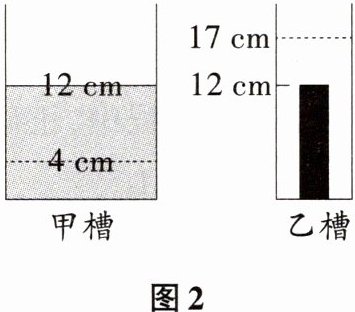
(2)如图2,若乙槽内放入高度为12 cm的圆柱形铁块,当甲槽内水位下降到4 cm时,乙槽内水位刚好到达铁块高度;当甲槽内的水全部注入乙槽时,乙槽的水位高度是17 cm.若乙槽的底面积是48 cm²,求甲槽的底面积和铁块的底面积;
(3)在(2)的条件下,是否存在乙槽水位高度是甲槽水位高度的4倍的情况?若存在,请求出此时甲槽的水位高度,若不存在,请说明理由.


(1)若甲槽的底面积是乙槽的2倍.
①当甲槽内水位下降x cm,则乙槽水位上升_______cm;(用含x的代数式表示)
②当甲槽与乙槽水位高度相等时,求水槽中水位的高度;
(2)如图2,若乙槽内放入高度为12 cm的圆柱形铁块,当甲槽内水位下降到4 cm时,乙槽内水位刚好到达铁块高度;当甲槽内的水全部注入乙槽时,乙槽的水位高度是17 cm.若乙槽的底面积是48 cm²,求甲槽的底面积和铁块的底面积;
(3)在(2)的条件下,是否存在乙槽水位高度是甲槽水位高度的4倍的情况?若存在,请求出此时甲槽的水位高度,若不存在,请说明理由.
答案:
解:
(1)①2x 提示:
∵甲槽的底面积是乙槽的2倍,甲槽内减少的水的体积等于乙槽内增加的水的体积,
∴当甲槽内水位下降x cm时,乙槽水位上升2x cm. ②由①知,甲槽内水位下降x cm时,乙槽水位上升2x cm,根据题意,得12 - x = 2x,解得x = 4,则12 - 4 = 8(cm). 答:当甲槽与乙槽水位高度相等时,水槽中水位的高度为8 cm.
(2)由题意知,乙槽水位上升17 - 12 = 5(cm),甲槽水位下降4 cm.
∵乙槽的底面积是48 cm²,
∴甲槽底面积为$\frac{48×5}{4}$ = 60(cm²). 设铁块的底面积为a cm²,根据题意,得60×(12 - 4) = (48 - a)×12,解得a = 8. 答:甲槽的底面积为60 cm²,铁块的底面积为8 cm².
(3)
∵当甲槽内的水位高度为4 cm时,乙槽内的水位高度为12 cm,此时高度比为1∶3,
∴只有当甲槽水位高度低于4 cm,乙槽水位高度高于12 cm时,才可能使乙槽水位高度是甲槽水位高度的4倍. 设甲槽水位高度为y cm,则乙槽的水位高度为4y cm,根据题意,得60y + 48×4y - 8×12 = 60×12,解得y = $\frac{68}{21}$. 答:存在乙槽水位高度是甲槽水位高度的4倍的情况,此时甲槽的水位高度为$\frac{68}{21}$ cm.
(1)①2x 提示:
∵甲槽的底面积是乙槽的2倍,甲槽内减少的水的体积等于乙槽内增加的水的体积,
∴当甲槽内水位下降x cm时,乙槽水位上升2x cm. ②由①知,甲槽内水位下降x cm时,乙槽水位上升2x cm,根据题意,得12 - x = 2x,解得x = 4,则12 - 4 = 8(cm). 答:当甲槽与乙槽水位高度相等时,水槽中水位的高度为8 cm.
(2)由题意知,乙槽水位上升17 - 12 = 5(cm),甲槽水位下降4 cm.
∵乙槽的底面积是48 cm²,
∴甲槽底面积为$\frac{48×5}{4}$ = 60(cm²). 设铁块的底面积为a cm²,根据题意,得60×(12 - 4) = (48 - a)×12,解得a = 8. 答:甲槽的底面积为60 cm²,铁块的底面积为8 cm².
(3)
∵当甲槽内的水位高度为4 cm时,乙槽内的水位高度为12 cm,此时高度比为1∶3,
∴只有当甲槽水位高度低于4 cm,乙槽水位高度高于12 cm时,才可能使乙槽水位高度是甲槽水位高度的4倍. 设甲槽水位高度为y cm,则乙槽的水位高度为4y cm,根据题意,得60y + 48×4y - 8×12 = 60×12,解得y = $\frac{68}{21}$. 答:存在乙槽水位高度是甲槽水位高度的4倍的情况,此时甲槽的水位高度为$\frac{68}{21}$ cm.
查看更多完整答案,请扫码查看


