《2025年初中学霸创新题七年级数学下册华师大版》

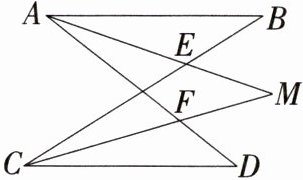
4 如图，AM、CM分别平分∠BAD和∠BCD，AM与BC交于点E，AD与CM交于点F，若∠B=32°，∠D=38°，求∠M的度数.

答案： 解：由题意知，∠BAM + ∠B + ∠AEB = ∠BCM + ∠M + ∠CEM = 180°，∠DCM + ∠D + ∠CFD = ∠DAM + ∠M + ∠AFM = 180°， 又因为∠AEB = ∠CEM，∠CFD = ∠AFM， 所以∠BAM + ∠B = ∠BCM + ∠M，∠DCM + ∠D = ∠DAM + ∠M， 所以∠BAM + ∠B + ∠DCM + ∠D = ∠BCM + ∠M + ∠DAM + ∠M。 因为AM、CM分别平分∠BAD和∠BCD， 所以∠BAM = ∠DAM，∠DCM = ∠BCM， 所以∠DAM + ∠B + ∠BCM + ∠D = ∠BCM + ∠M + ∠DAM + ∠M， 即∠B + ∠D = ∠M + ∠M，所以∠M = $\frac{32° + 38°}{2}$ = 35°。

5（河南郑州郑东新区校级期中）如图，在△ABC中，∠A=60°，BD、CD分别平分∠ABC和∠ACB，BE、CE分别平分∠DBC和∠DCB，则∠BEC等于（ ）

A. 140°
B. 150°
C. 165°
D. 170°

答案： 解析：因为∠A = 60°，所以∠ABC + ∠ACB = 180° - 60° = 120°。 因为BD、CD分别平分∠ABC和∠ACB， 所以∠DBC = $\frac{1}{2}$∠ABC，∠DCB = $\frac{1}{2}$∠ACB， 所以∠DBC + ∠DCB = $\frac{1}{2}$(∠ABC + ∠ACB) = 60°。 因为BE、CE分别平分∠DBC和∠DCB， 所以∠EBC = $\frac{1}{2}$∠DBC，∠ECB = $\frac{1}{2}$∠DCB， 所以∠EBC + ∠ECB = $\frac{1}{2}$(∠DBC + ∠DCB) = 30°， 所以∠BEC = 180° - (∠EBC + ∠ECB) = 150°。故选B。

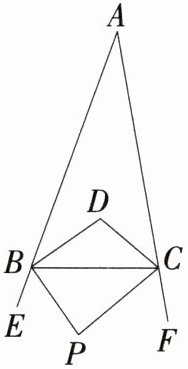
6【新趋势·探究性问题】如图，在△ABC中，BD、CD分别是∠ABC、∠ACB的平分线，BP、CP分别是∠EBC、∠FCB的平分线.
(1) 若∠A=30°，直接写出∠BDC、∠BPC的度数；
(2) 当∠A变化时，∠D+∠P的值是否变化？请说明理由.

答案： 解：
(1)在△ABC中，∠ABC + ∠ACB = 180° - ∠A。因为BD、CD分别是∠ABC和∠ACB的平分线，所以∠DBC = $\frac{1}{2}$∠ABC，∠DCB = $\frac{1}{2}$∠ACB，所以∠DBC + ∠DCB = $\frac{1}{2}$(∠ABC + ∠ACB) = $\frac{1}{2}$(180° - ∠A) = 90° - $\frac{1}{2}$∠A，所以∠BDC = 180° - (∠DBC + ∠DCB) = 180° - (90° - $\frac{1}{2}$∠A) = 90° + $\frac{1}{2}$∠A。 因为∠A = 30°，所以∠BDC = 90° + $\frac{1}{2}$×30° = 105°。 因为BP、CP分别是∠EBC、∠FCB的平分线， 所以∠CBP = $\frac{1}{2}$∠EBC，∠BCP = $\frac{1}{2}$∠FCB，所以∠CBP + ∠BCP = $\frac{1}{2}$∠EBC + $\frac{1}{2}$∠FCB = $\frac{1}{2}$(∠EBC + ∠FCB)。 又因为∠EBC、∠FCB是△ABC的外角，所以∠CBP + ∠BCP = $\frac{1}{2}$(∠A + ∠ACB + ∠A + ∠ABC) = $\frac{1}{2}$(180° + ∠A)， 所以∠BPC = 180° - (∠CBP + ∠BCP) = 180° - $\frac{1}{2}$(180° + ∠A) = 90° - $\frac{1}{2}$∠A。因为∠A = 30°，所以∠BPC = 90° - $\frac{1}{2}$×30° = 75°。
(2)∠D + ∠P的值不变。理由如下： 因为由
(1)知，∠D = 90° + $\frac{1}{2}$∠A，∠P = 90° - $\frac{1}{2}$∠A，所以∠D + ∠P = 180°。即当∠A变化时，∠D + ∠P的值不变。