《2025年初中学霸创新题七年级数学下册华师大版》

1 下列方程中，属于一元一次方程的是 （ ）
A. $x - 3 = y$
B. $x^{2}-1 = 3$
C. $x - 2 = 3$
D. $\frac{2}{x}=3$

答案： C 解析：A选项中，有两个未知数，故方程不是一元一次方程；B选项中，未知数的次数不是1，故方程不是一元一次方程；D选项中，未知数位于分母处，含未知数的式子不是整式，故方程不是一元一次方程；C选项中，方程是一元一次方程。故选C。

2 下列结论正确的有 （ ）
①若$ac = d = bc + d$，则$a = b$；
②若$a = b$，则$\frac{a}{c^{2}+1}=\frac{b}{c^{2}+1}$；
③若$a + cd = b + cd$，则$a = b$；
④若$a = b$，则$a^{2}=b^{2}$.
A. 1个
B. 2个
C. 3个
D. 4个

答案： C 解析：①ac + d = bc + d，两边都减去d，得ac = bc，若c = 0，则不能推出a = b，故①错误；②a = b，c² + 1 ≠ 0，两边都除以(c² + 1)，得$\frac{a}{c² + 1}$ = $\frac{b}{c² + 1}$，故②正确；③a + cd = b + cd，两边都减去cd，得a = b，故③正确；④a = b，可以推出a² = b²，故④正确。 故选C。

3（河南新乡原阳阶段练习）小李在解关于x的方程$5a - x = 13$时（其中a为已知数），误将“-x”中的“-”看成“+”，得方程的解为$x = - 2$，则原方程的解为 （ ）
A. $x = 3$
B. $x = 0$
C. $x = 2$
D. $x = 1$

答案： C 解析：将x = - 2代入“看错的”方程5a + x = 13，得5a - 2 = 13，解得a = 3，所以原方程为5×3 - x = 13，解得x = 2，故原方程的解为x = 2. 故选C。

4 数学课上，老师让大家求单项式$-2a^{m + 2}b^{2}$与单项式$3a^{-3m - 2}b^{2}$的和，同学们计算后发现其和仍是一个单项式，则m的值是 （ ）
A. - 1
B. 0
C. 1
D. - 2

答案： A 解析：因为单项式 - 2a^(m + 2)b²与3a^(- 3m - 2)b²的和仍是单项式，所以两个单项式是同类项，即m + 2 = - 3m - 2，解得m = - 1. 故选A。→相同字母的指数相等。

5【新情境·数学文化】《孙子算经》是我国古代重要的数学著作，是《算经十书》之一，书中记载了这样一个题目：今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？其大意是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余1尺，问木长多少尺？设木长x尺，则可列方程为 （ ）
A. $\frac{1}{2}(x + 4.5)=x - 1$
B. $\frac{1}{2}(x + 4.5)=x + 1$
C. $\frac{1}{2}(x + 1)=x - 4.5$
D. $\frac{1}{2}(x - 1)=x + 4.5$

答案： A 解析：木长x尺，由“用一根绳子去量一根长木，绳子还剩余4.5尺”，可知绳长(x + 4.5)尺；由“将绳子对折再量长木，长木还剩余1尺”，可知绳长2(x - 1)尺，则可列方程x + 4.5 = 2(x - 1)，即$\frac{1}{2}$(x + 4.5) = x - 1. 故选A。

6（四川攀枝花仁和期末）已知关于x的方程$3x = x + a$的解与$\frac{x + 1}{2}=x+\frac{1}{4}$的解相同，则a的值为 （ ）
A. 1
B. - 1
C. 2
D. - 2

答案： A 解析：解方程$\frac{x + 1}{2}$ = x + $\frac{1}{4}$，得x = $\frac{1}{2}$.
∵两个方程的解相同，
∴将x = $\frac{1}{2}$代入方程3x = x + a，解得a = 1. 故选A。

7（河南南阳方城期中）某服装店分别用100元的价格卖出了两件服装，其中一件盈利20%，另一件亏损20%，那么该服装店卖出这两件服装的盈利情况是 （ ）
A. 盈利
B. 亏损
C. 不盈不亏
D. 无法确定

答案： B 解析：设盈利的服装的进价为x元， 根据题意，得(1 + 20%)x = 100，解得x = $\frac{250}{3}$. 设亏损的服装的进价为y元， 根据题意，得(1 - 20%)y = 100，解得y = 125. 故该服装店卖出这两件服装一共盈利100×2 - $\frac{250}{3}$ - 125 ≈ - 8.3(元)，即亏损。故选B。

8（北京海淀校级期中）按下面的程序计算：

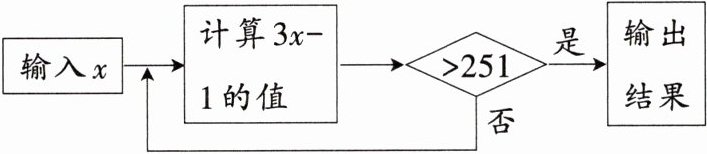
如果输入x的值是正整数，输出结果是257，那么满足条件的x的值有 （ ）
A. 1个
B. 2个
C. 3个
D. 4个

答案： C 解析：因为输出的结果为257，所以3x - 1 = 257，解得x = 86；令3x - 1 = 86，解得x = 29；令3x - 1 = 29，解得x = 10；令3x - 1 = 10，解得x = $\frac{11}{3}$(不符合题意，舍去)，故满足条件的x的值有86、29、10，共3个。故选C。

9【新定义·新运算问题】我们定义一种运算：$a*b = ab + 2a - b$，若$3*x = 12$，则$x =$_______.

答案： 3 解析：因为a*b = ab + 2a - b， 所以3*x = 3x + 2×3 - x = 12，即3x + 6 - x = 12， 解得x = 3.

10【新趋势·规律探究题】有一列数，按一定的规律排列成$\frac{1}{3},-1,3,-9,27,-81,\cdots$. 若其中某三个相邻数的和是-567，则这三个数中第一个数是_______.

答案： - 81 解析：设这三个数中的第一个数为x，则另外两个数分别为 - 3x，9x，根据题意，得x - 3x + 9x = - 567，解得x = - 81.

11【新情境·数学文化】幻方历史悠久，传说最早出现在夏禹时代的“洛书”. 把洛书用今天的数学符号翻译出来，就是一个三阶幻方，将数字1～9分别填入如图所示的幻方中，要求每一横行、每一竖列以及两条对角线上的数字之和都是15，则a的值为_______.

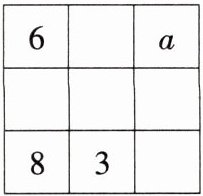
答案： 2 解析：设右下角方格内的数字为b，
∵每一横行的数字之和都是15，
∴8 + 3 + b = 15，即b = 4.
∵两条对角线上的数字之和都是15，
∴6 + b = 8 + a，即6 + 4 = 8 + a，
∴a = 2.

12（一题多解）如果不论k为何值，$x = - 1$总是关于x的方程$\frac{kx + a}{2}-\frac{2x - bk}{3}=1$的解，则$a =$_______，$b =$_______.

答案： $\frac{2}{3}$ $\frac{3}{2}$ 解析：解法一：将x = - 1代入原方程，得$\frac{- k + a}{2}$ - $\frac{- 2 - bk}{3}$ = 1，去分母，得3(- k + a) - 2(- 2 - bk) = 6， 去括号，得 - 3k + 3a + 4 + 2bk = 6， 移项、合并同类项，得(2b - 3)k = 2 - 3a.
∵对任意的k上式都成立，
∴2b - 3 = 0，2 - 3a = 0， 解得a = $\frac{2}{3}$，b = $\frac{3}{2}$. 解法二(特殊值法)：
∵不论k取何值，x = - 1总是方程$\frac{kx + a}{2}$ - $\frac{2x - bk}{3}$ = 1的解，
∴将x = - 1代入原方程，得$\frac{- k + a}{2}$ - $\frac{- 2 - bk}{3}$ = 1，即(2b - 3)k = 2 - 3a. 将k = 0代入(2b - 3)k = 2 - 3a，得a = $\frac{2}{3}$. 将k = 1，a = $\frac{2}{3}$代入(2b - 3)k = 2 - 3a，得b = $\frac{3}{2}$.