《2025年初中学霸创新题七年级数学下册华师大版》

1 下列为一元一次不等式的是 （ ）
A. x+y＞−2
B. $\dfrac{1}{x} + 3 ＜ 2$
C. −2x=7
D. $\dfrac{x}{5} + \dfrac{x}{2} \geqslant 1$

答案： D

2（吉林长春宽城期中）若a＞b，下列不等式不一定成立的是 （ ）
A. a−5＞b−5
B. −5a＜−5b
C. $\dfrac{a}{c} ＞ \dfrac{b}{c}$
D. a+c＞b+c

答案： C

3（河南周口期末）下列说法中正确的是（ ）
A. x=1是不等式2x＜3的一个解
B. x=1是不等式2x＜3的解集
C. x=1是不等式2x＜3的唯一解
D. x=1不是不等式2x＜3的解

答案： A

4（浙江中考）不等式组$\begin{cases}2x - 1 \geqslant 1, \\ 3(2 - x) ＞ - 6\end{cases}$的解集在数轴上表示为 （ ）

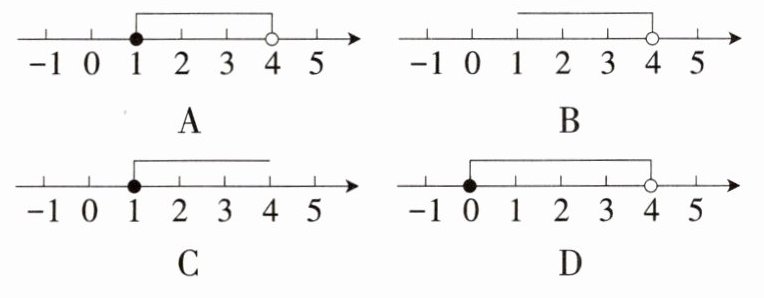
答案： A

5 若方程组$\begin{cases}2x + 3y = a - 1, \\ 3x + 2y = 6\end{cases}$的解满足1＜x+y＜2，则a的取值范围是 （ ）
A. 0＜a＜5
B. 0＜a＜2
C. 5＜a＜10
D. a＞0

答案： A

6【新定义·新运算问题】定义新运算：对于任意有理数a、b都有a⊕b=a(a−b)+1，如：2⊕5=2×(2−5)+1=−5，那么不等式4⊕x≥2的正整数解的个数是 （ ）
A. 1
B. 2
C. 3
D. 4

答案： C

7 若ax−b＞0的解集是x＜−2，则bx+a＞0的解集是 （ ）
A. x＞2
B. x＜2
C. x＞$\dfrac{1}{2}$
D. x＜$\dfrac{1}{2}$

答案： C

8 若关于x的一元一次方程3x−2=x−m有整数解，且关于y的不等式组$\begin{cases}-2y + 1 ＜ 5, \\ 3 - m ＞ 5y - 1\end{cases}$有且只有三个整数解，则满足所有条件的整数m的和是 （ ）
A. −6
B. 6
C. 12
D. −12

答案： D

9（山西临汾尧都期末）“x的3倍与5的差不大于4”，用不等式表示为_______.

答案： 3x - 5 \leq 4

10（河南新乡原阳期末）不等式2x−3≥0的最小整数解是_______.

答案： 2

11【新趋势·开放性问题】若不等式组$\begin{cases}-x - 1 \leqslant 0, \\ x□3 ＜ 0\end{cases}$有解，则□中的运算符号可以是_______.（写出一个即可）

答案： -（答案不唯一）

12 如图，若满足输出值y＞100，则输入的正整数x的最小值为_______.

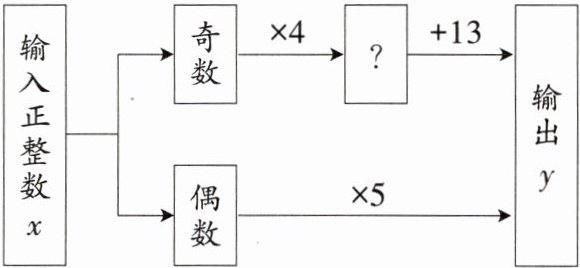
答案： 22

13（河南开封阶段练习）若关于x的不等式组$\begin{cases}x + 2m ＜ 0, \\ 3x + m ＜ 15\end{cases}$的解集中的任意x的值，都能使不等式x−3＜0成立，则m的取值范围是_______.

答案： m \geq -\frac{3}{2}