《2025年初中学霸创新题七年级数学下册华师大版》

1（湖南衡阳中考）下列长度的各组线段能组成一个三角形的是 ( )
A. 1 cm,2 cm,3 cm
B. 3 cm,8 cm,5 cm
C. 4 cm,5 cm,10 cm
D. 4 cm,5 cm,6 cm

答案： **D** 解析： - A. $1\mathrm{cm},2\mathrm{cm},3\mathrm{cm}$，因为$1 + 2=3$，不能组成三角形； - B. $3\mathrm{cm},8\mathrm{cm},5\mathrm{cm}$，$3 + 5=8$，不能组成三角形； - C. $4\mathrm{cm},5\mathrm{cm},10\mathrm{cm}$，$4 + 5\lt10$，不能组成三角形； - D. $4\mathrm{cm},5\mathrm{cm},6\mathrm{cm}$，$4 + 5\gt6$，能组成三角形. 故选 D. - **解题关键点**：判断三条线段能否组成三角形，可以将较短的两条线段长度相加，若大于第三条线段的长度，则可以组成三角形，反之则不能.

2（河南南阳南召期末）长度为2 cm,3 cm,4 cm,5 cm的4条线段,若以其中的三条线段为边构成三角形,可以构成不同的三角形共有 ( )
A. 1个
B. 2个
C. 3个
D. 4个

答案： **C** 解析：$2\mathrm{cm},3\mathrm{cm},4\mathrm{cm}$可以构成三角形；$2\mathrm{cm},4\mathrm{cm},5\mathrm{cm}$可以构成三角形；$3\mathrm{cm},4\mathrm{cm},5\mathrm{cm}$可以构成三角形，所以可以构成 3 个不同的三角形. 故选 C.

3【新趋势·五育文化】初中生体能训练中有一项跳跃泥潭障碍训练,如图,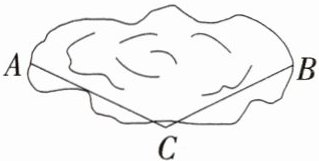
小刚平时助跑跳跃距离约为(4.5±0.1) m,他不确定自己是否能够跳过这个泥潭(AB的长度),于是测量了相关长度,由于米尺长度有限,小刚测得AC=2.1 m,BC=2 m,根据小刚的测量,他______完成这项训练挑战.（填“能”或“不能”）

答案： **能** 解析：由题意可知，$AB\lt AC + BC=2.1+2 = 4.1(\mathrm{m})\lt4.5 - 0.1 = 4.4(\mathrm{m})$，所以小明能完成这项训练挑战.

4 已知三角形两边长分别为1、5,第三边的长为整数,则第三边的长为______.

答案： **5** 解析：设三角形第三边的长为$x$，则$5 - 1\lt x\lt5 + 1$，即$4\lt x\lt6$. 因为第三边的长为整数，所以$x = 5$.

【变式】 已知△ABC的三边长均为整数,且其中两边的长分别为3和5,则这个三角形的周长为______.

答案： **【变式】** $11$或$12$或$13$或$14$或$15$ 解析：因为$\triangle ABC$其中两边的长分别为 3 和 5，设第三边的长为$x$，所以$5 - 3\lt x\lt5 + 3$，即$2\lt x\lt8$. 因为$\triangle ABC$的三边长均为整数，所以第三边的长为 3 或 4 或 5 或 6 或 7，所以这个三角形的周长为 11 或 12 或 13 或 14 或 15.

5（教材P91第2题改编）若△ABC(三边长度各不相同)的周长为18,其中一条边长为4,则△ABC中的最长边x的取值范围为______.

答案： **$7\lt x\lt9$** 解析：因为$\triangle ABC$的周长为 18，其中一条边长为 4，最长边为$x$，所以第三边的长为$18 - 4 - x=14 - x$，所以$x\gt4$且$x\gt14 - x$，解得$x\gt7$. 根据三角形的三边关系，得$x\lt14 - x+4$，解得$x\lt9$，所以$7\lt x\lt9$.

6（易错题）（河南洛阳模拟）已知一等腰三角形的两边长x、y满足方程组$\begin{cases}2x - y = 3,\\3x + 2y = 8,\end{cases}$则此等腰三角形的周长为______.

答案： **5** 解析：解方程组$\begin{cases}2x - y = 3\\3x + 2y = 8\end{cases}$，得$\begin{cases}x = 2\\y = 1\end{cases}$，所以等腰三角形的两边长为 2、1，分情况讨论如下： -
(1)若腰长为 1，则等腰三角形的三边长为 1、1、2，$1 + 1=2$，不能组成三角形； -
(2)若腰长为 2，则等腰三角形的三边长为 2、2、1，能组成三角形，且三角形的周长为 5. - 综上所述，这个等腰三角形的周长为 5. - **易错点**：注意要分两种情况讨论，并利用三角形的三边关系检验能否组成三角形，易因忽略分情况讨论或检验而出错.

7 某市木材市场上木棒规格与价格如下表,小明的爷爷要做一个三角形的支架养鱼用,现有两根长度分别为3 m和5 m的木棒,还需要到该木材市场上购买一根.

(1)有几种规格的木棒可供小明的爷爷选择?
(2)在能做成三角形支架的情况下,选择哪一种规格的木棒最省钱?

答案： 解： -
(1)设第三根木棒的长度为$x\mathrm{m}$，根据三角形的三边关系，可得$5 - 3\lt x\lt5 + 3$，解得$2\lt x\lt8$，所以$x = 3、4、5、6$，共 4 种，所以有 4 种规格的木棒可供小明的爷爷选择. -
(2)根据木棒的价格可得，选$3\mathrm{m}$的木棒最省钱.

8【新情境·人体健康】双人漫步机是一种有氧运动器材,通过进行中等强度的有氧运动,如慢跑、快走等,可以增强人体的心肺功能,降低血压、改善血糖. 如图,这种支架设计应用的几何原理是 ( )

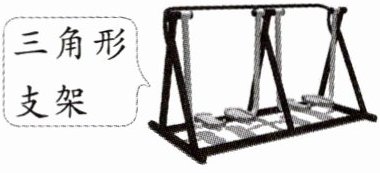
A. 三角形的稳定性
B. 两点之间线段最短
C. 两点确定一条直线
D. 垂线段最短

答案： **A**

9（河南驻马店汝南期中）下列生产和生活实例：①用人字架来建筑房屋;②用窗钩来固定窗扇;③在栅栏门上斜钉着一根木条;④商店的推拉活动防盗门. 其中,用到三角形的稳定性的有______.（填写序号）

答案： **①②③** 解析：商店的推拉活动防盗门，是利用四边形的不稳定性，不是利用三角形的稳定性，所以用到三角形稳定性的有①②③.