《2025年学习指要九年级数学上册人教版》

2.(2024 重庆二模)在正方形 $ABCD$ 中,将 $AB$ 绕点 $A$ 逆时针旋转 $\alpha$ 到 $AE$,连接 $BE$,并延长至点 $F$,使 $CF = CB$,连接 $DF$,则 $\angle DFC$ 的度数是(A)

A.$45^{\circ}+\frac{\alpha}{2}$
B.$45^{\circ}+\alpha$
C.$90^{\circ}-\frac{\alpha}{2}$
D.$2\alpha - 45^{\circ}$

答案： A

3. 如图,将 $\triangle AOB$ 绕点 $O$ 按逆时针方向旋转 $45^{\circ}$ 后得到 $\triangle COD$,若 $\angle AOB = 15^{\circ}$,则 $\angle AOD$ 的度数是$60^{\circ}$。

答案： 【解析】：
根据旋转的性质，$\triangle AOB$绕点$O$逆时针旋转$45^{\circ}$后得到$\triangle COD$。
因此，$\angle BOD = 45^{\circ}$。
已知$\angle AOB = 15^{\circ}$。
所以$\angle AOD = \angle AOB + \angle BOD = 15^{\circ} + 45^{\circ} = 60^{\circ}$。
【答案】：$60^{\circ}$

4.(2024 开州区阶段练习)如图,将 $\triangle ABC$ 绕点 $A$ 顺时针旋转得到 $\triangle ADE$,点 $C$ 的对应点 $E$ 落在 $CB$ 的延长线上,连接 $BD$。若 $BD = 5$,$DE = 3$,$CE = 7$,则 $AE = $$\frac{7\sqrt{2}}{2}$。

答案：
∵△ABC绕点A顺时针旋转得到△ADE，
∴△ABC≌△ADE，
∴AB=AD，AC=AE，BC=DE=3，∠BAD=∠CAE。
∵点E在CB延长线上，CE=7，BC=3，
∴EB=CE-BC=7-3=4。
∵DE=3，EB=4，BD=5，
∴DE²+EB²=3²+4²=25=BD²，
∴△BDE是直角三角形，∠BED=90°。
∵AB=AD，AC=AE，∠BAD=∠CAE，
∴△ABD∽△ACE（等腰三角形顶角相等则相似），
∴AB/AC=BD/CE=5/7，设AB=AD=5k，AC=AE=7k。
过A作AF⊥EC于F，
∵AC=AE，
∴F为EC中点（等腰三角形三线合一），
∴EF=FC=7/2，FB=EF-EB=7/2-4=1/2。
在Rt△AFE中，AF²=AE²-EF²=(7k)²-(7/2)²；在Rt△AFB中，AF²=AB²-FB²=(5k)²-(1/2)²。
∴(7k)²-(7/2)²=(5k)²-(1/2)²，解得k=√2/2。
∴AE=7k=7×√2/2=7√2/2。
7√2/2

5.(2023 宜昌中考)如图,在方格纸中按要求画图,并填空。
(1)画出线段 $OA$ 绕点 $O$ 顺时针旋转 $90^{\circ}$ 后得到的线段 $OB$,连接 $AB$；
(2)画出与 $\triangle AOB$ 关于直线 $OB$ 对称的图形,点 $A$ 的对称点是点 $C$；
(3)$\angle OCB$ 的度数为______。

(1) 图略（按要求画出线段OB及AB）；
(2) 图略（按要求画出△COB，其中C为A关于OB的对称点）；
(3) 45°

答案：
(1) 图略（按要求画出线段OB及AB）；
(2) 图略（按要求画出△COB，其中C为A关于OB的对称点）；
(3) 45°

6.(2024 涪陵区阶段练习)如图,在四边形 $ABCD$ 中,将 $\triangle ABC$ 绕点 $C$ 顺时针旋转 $60^{\circ}$ 得到 $\triangle EDC$,此时 $A$,$D$,$E$ 三点恰好共线。已知 $AB = 5$,$AD = 3$。
(1)求 $AC$ 的长；
(2)求证：$AC$ 平分 $\angle BAE$。

答案：
(1)由旋转性质得：$AC=EC$，$\angle ACE=60°$，$AB=ED=5$。
∵$A$，$D$，$E$三点共线，
∴$AE=AD+DE=3+5=8$。
在$\triangle ACE$中，$AC=EC$，$\angle ACE=60°$，
∴$\triangle ACE$是等边三角形，
∴$AC=AE=8$。
(2)
∵$\triangle ACE$是等边三角形，
∴$\angle CAE=60°$。
由旋转性质得：$\angle BAC=\angle DEC$。
∵$A$，$D$，$E$三点共线，
∴$\angle DEC=\angle AEC$。
∵$\triangle ACE$是等边三角形，
∴$\angle AEC=60°$，
∴$\angle DEC=60°$。
∴$\angle BAC=60°$，
∴$\angle BAC=\angle CAE$，即$AC$平分$\angle BAE$。
(1)$8$；
(2)证明见上。

7.(2023 巴南区期末)如图,在四边形 $ABCD$ 中,$AC$,$BD$ 是对角线,$\triangle ABC$ 是等边三角形,线段 $CD$ 绕点 $C$ 顺时针旋转 $60^{\circ}$ 得到线段 $CE$,连接 $AE$,$DE$。
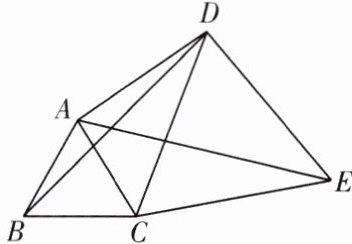
(1)求证：$\angle CBD = \angle CAE$；
(2)若 $\angle ADC = 30^{\circ}$,$AD = 3$,$BD = 5$,求 $DE$ 的长。

答案：
(2) $\boxed{4}$