第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
例 1 如图,某小区准备在长为 $(4a + 3b)$ 米,宽为 $(2a + 3b)$ 米的长方形草坪上修建一横两竖,宽度均为 $b$ 米的人行通道(图中阴影部分)。
(1)求该通道的面积共有多少平方米?
(2)若 $a = 2b$,剩余草坪的面积是 $216$ 平方米,求通道的宽度。
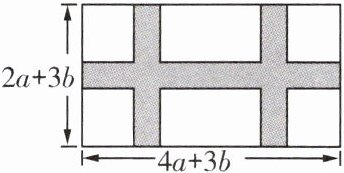
名师导引 (1)通道面积问题可以先利用平移法把竖直通道平移到左侧或右侧,水平通道平移到上面或下面,用代数式表示通道的面积;(2)通道的面积等于三个通道面积之和减去它们重叠部分的小正方形面积。
(1)求该通道的面积共有多少平方米?
(2)若 $a = 2b$,剩余草坪的面积是 $216$ 平方米,求通道的宽度。

名师导引 (1)通道面积问题可以先利用平移法把竖直通道平移到左侧或右侧,水平通道平移到上面或下面,用代数式表示通道的面积;(2)通道的面积等于三个通道面积之和减去它们重叠部分的小正方形面积。
答案:
(1)横通道面积:$(4a+3b)\cdot b$,两个竖通道面积:$2\cdot (2a+3b)\cdot b$,重叠部分面积:$2b^2$(2个边长为$b$的正方形)。
通道总面积$S=(4a+3b)b + 2(2a+3b)b - 2b^2$
$=4ab+3b^2 + 4ab+6b^2 - 2b^2$
$=8ab+7b^2$
答:通道面积为$(8ab + 7b^2)$平方米。
(2)剩余草坪面积$=$原草坪面积$-$通道面积,由平移法得剩余草坪长为$(4a+3b - 2b)=4a+b$,宽为$(2a+3b - b)=2a+2b$,故剩余面积$(4a+b)(2a+2b)$。
当$a=2b$时,$4a+b=9b$,$2a+2b=6b$,剩余面积$9b\cdot6b=54b^2$。
由$54b^2=216$,得$b^2=4$,$b=2$($b=-2$舍去)。
答:通道宽度为$2$米。
(1)横通道面积:$(4a+3b)\cdot b$,两个竖通道面积:$2\cdot (2a+3b)\cdot b$,重叠部分面积:$2b^2$(2个边长为$b$的正方形)。
通道总面积$S=(4a+3b)b + 2(2a+3b)b - 2b^2$
$=4ab+3b^2 + 4ab+6b^2 - 2b^2$
$=8ab+7b^2$
答:通道面积为$(8ab + 7b^2)$平方米。
(2)剩余草坪面积$=$原草坪面积$-$通道面积,由平移法得剩余草坪长为$(4a+3b - 2b)=4a+b$,宽为$(2a+3b - b)=2a+2b$,故剩余面积$(4a+b)(2a+2b)$。
当$a=2b$时,$4a+b=9b$,$2a+2b=6b$,剩余面积$9b\cdot6b=54b^2$。
由$54b^2=216$,得$b^2=4$,$b=2$($b=-2$舍去)。
答:通道宽度为$2$米。
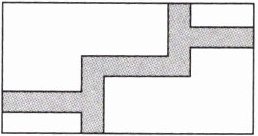
变式训练 (2024 萨迦一模)如图,在宽为 $20$ 米、长为 $32$ 米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪。要使草坪的面积为 $540$ 平方米,则道路的宽为(
A.$5$ 米
B.$3$ 米
C.$2$ 米
D.$2$ 米或 $5$ 米
C
)
A.$5$ 米
B.$3$ 米
C.$2$ 米
D.$2$ 米或 $5$ 米
答案:
C
例 2 为培养学生正确的劳动价值观和良好的劳动品质,某校规划修建矩形苗圃 $ABCD$,如图。苗圃的一边靠墙(墙最大可用长度为 $15\ m$),另三边用木栏围成,中间用垂直于墙的木栏隔开分成面积相等的两个区域,并在如图所示的两处各留 $1\ m$ 宽的门(门不用木栏),修建所用木栏总长为 $28\ m$。
(1)若矩形 $ABCD$ 的面积为 $72\ m^2$,求 $AB$ 的长;
(2)矩形 $ABCD$ 的面积能否为 $80\ m^2$,若能,求出 $AB$ 的长;若不能,说明理由。
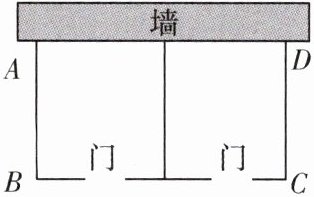
名师导引 在这类面积问题中,要考虑矩形的长和宽的取值范围,尤其是平行于墙的边的长度不能大于墙的长度;当 $\Delta < 0$ 时,方程没有实数根。
(1)若矩形 $ABCD$ 的面积为 $72\ m^2$,求 $AB$ 的长;
(2)矩形 $ABCD$ 的面积能否为 $80\ m^2$,若能,求出 $AB$ 的长;若不能,说明理由。

名师导引 在这类面积问题中,要考虑矩形的长和宽的取值范围,尤其是平行于墙的边的长度不能大于墙的长度;当 $\Delta < 0$ 时,方程没有实数根。
答案:
设垂直墙的一边$AB$的长为$x$米,
因为两处各留$1m$宽的门,且中间木栏垂直于墙,
所以平行于墙的一边$AD = (28 + 2 - 3x)= (30 - 3x)$米。
(1)由题意得$(30 - 3x)x = 72$,
即$x^{2}-10x + 24 = 0$,
分解因式得$(x - 4)(x - 6)=0$,
解得$x_{1}= 4$,$x_{2}= 6$。
当$x = 4$时,$30 - 3x = 18>15$,不符合题意,舍去;
当$x = 6$时,$30 - 3x = 12<15$,符合题意。
所以$AB$的长为$6$米。
(2)由题意得$(30 - 3x)x = 80$,
即$3x^{2}-30x + 80 = 0$,
其中$\Delta=(-30)^{2}-4×3×80 = 900 - 960=-60<0$,
所以此方程无实数根。
所以矩形$ABCD$的面积不能为$80m^{2}$。
因为两处各留$1m$宽的门,且中间木栏垂直于墙,
所以平行于墙的一边$AD = (28 + 2 - 3x)= (30 - 3x)$米。
(1)由题意得$(30 - 3x)x = 72$,
即$x^{2}-10x + 24 = 0$,
分解因式得$(x - 4)(x - 6)=0$,
解得$x_{1}= 4$,$x_{2}= 6$。
当$x = 4$时,$30 - 3x = 18>15$,不符合题意,舍去;
当$x = 6$时,$30 - 3x = 12<15$,符合题意。
所以$AB$的长为$6$米。
(2)由题意得$(30 - 3x)x = 80$,
即$3x^{2}-30x + 80 = 0$,
其中$\Delta=(-30)^{2}-4×3×80 = 900 - 960=-60<0$,
所以此方程无实数根。
所以矩形$ABCD$的面积不能为$80m^{2}$。
变式训练 如图,某社区要修建一个面积为 $150\ m^2$ 的长方形花园 $ABCD$。为节省材料,花园的一边利用原有的一道墙,另三边用栅栏围成,$BC$ 边留有 $2\ m$ 的门 $EF$。如果所用栅栏的总长为 $33\ m$,且墙足够长,则花园的长和宽各为多少米?
答案:
设与墙垂直的一边长为 $ x \, m $,则与墙平行的一边长为 $ (35 - 2x) \, m $。
根据题意,面积为 $ 150 \, m^2 $,得:
$ x(35 - 2x) = 150 $
整理得:
$ 2x^2 - 35x + 150 = 0 $
解得:
$ x_1 = 10 $,$ x_2 = 7.5 $
当 $ x = 10 $ 时,与墙平行的边长为 $ 35 - 2 × 10 = 15 \, m $;
当 $ x = 7.5 $ 时,与墙平行的边长为 $ 35 - 2 × 7.5 = 20 \, m $。
答:花园的长为 $ 15 \, m $、宽为 $ 10 \, m $ 或长为 $ 20 \, m $、宽为 $ 7.5 \, m $。
根据题意,面积为 $ 150 \, m^2 $,得:
$ x(35 - 2x) = 150 $
整理得:
$ 2x^2 - 35x + 150 = 0 $
解得:
$ x_1 = 10 $,$ x_2 = 7.5 $
当 $ x = 10 $ 时,与墙平行的边长为 $ 35 - 2 × 10 = 15 \, m $;
当 $ x = 7.5 $ 时,与墙平行的边长为 $ 35 - 2 × 7.5 = 20 \, m $。
答:花园的长为 $ 15 \, m $、宽为 $ 10 \, m $ 或长为 $ 20 \, m $、宽为 $ 7.5 \, m $。
查看更多完整答案,请扫码查看


