第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. 把一个平面图形绕着平面内某一点 $O$ 转动一个角度,叫做图形的
旋转
。
答案:
旋转
2. 图形旋转的性质:旋转前后的图形
全等
;对应点到旋转中心的距离相等
;对应点与旋转中心所连线段的夹角等于旋转角
。
答案:
全等;相等;旋转角
思考 旋转的三个要素是什么?
练习(1)如果图形上的点 $P$ 经过旋转变为点 $P'$,那么这两点叫做这个旋转的
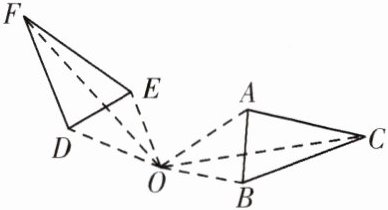
(2)如图,$\triangle ABC$ 绕着点 $O$ 旋转到 $\triangle DEF$ 的位置,则旋转中心是
旋转中心、旋转方向、旋转角度
练习(1)如果图形上的点 $P$ 经过旋转变为点 $P'$,那么这两点叫做这个旋转的
对应点
。(2)如图,$\triangle ABC$ 绕着点 $O$ 旋转到 $\triangle DEF$ 的位置,则旋转中心是
点O
,旋转角是∠AOD(或∠BOE或∠COF)
,$AO= $DO
,$AB= $DE
,$\angle ACB= $∠DFE
。
答案:
思考:旋转中心、旋转方向、旋转角度;
(1)对应点;
(2)点O;∠AOD(或∠BOE或∠COF);DO;DE;∠DFE
(1)对应点;
(2)点O;∠AOD(或∠BOE或∠COF);DO;DE;∠DFE
探究一 旋转的概念
例 1 如图 1,$\triangle ABC$ 为等边三角形,$D$ 为 $\triangle ABC$ 内一点,$\triangle ABD$ 经过旋转后到达 $\triangle ACP$ 的位置,则:(1)旋转中心是
名师导引 对应点与旋转中心所连线段的夹角为旋转角,找准旋转角是解决问题的关键。
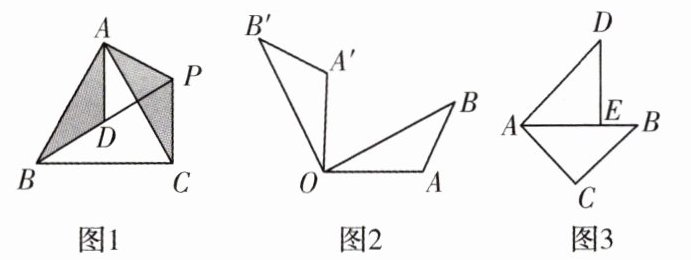
例 1 如图 1,$\triangle ABC$ 为等边三角形,$D$ 为 $\triangle ABC$ 内一点,$\triangle ABD$ 经过旋转后到达 $\triangle ACP$ 的位置,则:(1)旋转中心是
点$A$
;(2)旋转角度是$60°$
;(3)$\triangle ADP$ 是等边
三角形。名师导引 对应点与旋转中心所连线段的夹角为旋转角,找准旋转角是解决问题的关键。

答案:
(1)点$A$;
(2)$60°$;
(3)等边
(1)点$A$;
(2)$60°$;
(3)等边
变式训练(1)如图 2,$\triangle AOB$ 旋转到 $\triangle A'OB'$ 的位置。$\angle AOA' = 90^{\circ}$,则旋转中心是点
(2)如图 3,$\triangle ABC$ 与 $\triangle ADE$ 都是等腰直角三角形,$\angle C$ 和 $\angle AED$ 都是直角,点 $E$ 在 $AB$ 上,如果 $\triangle ABC$ 经旋转后能与 $\triangle ADE$ 重合,那么旋转中心是点
O
,旋转角是90°
。点 $A$ 的对应点是A'
,线段 $AB$ 的对应线段是A'B'
,$\angle B$ 的对应角是∠B'
,$\angle BOB' = $90°
。(2)如图 3,$\triangle ABC$ 与 $\triangle ADE$ 都是等腰直角三角形,$\angle C$ 和 $\angle AED$ 都是直角,点 $E$ 在 $AB$ 上,如果 $\triangle ABC$ 经旋转后能与 $\triangle ADE$ 重合,那么旋转中心是点
A
,旋转的度数是45°
。
答案:
(1) O;90°;A';A'B';∠B';90°
(2) A;45°
(1) O;90°;A';A'B';∠B';90°
(2) A;45°
探究二 旋转的性质
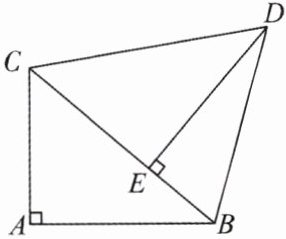
例 2(2024 巴南区阶段练习改编)如图,$Rt\triangle ABC$ 中,$\angle A = 90^{\circ}$,$\angle ABC = \alpha$,将 $Rt\triangle ABC$ 绕点 $C$ 逆时针旋转得到 $Rt\triangle EDC$,点 $A$ 的对应点 $E$ 正好落在 $BC$ 上,连接 $BD$,则 $\angle CBD$ 的度数是
名师导引 注意运用旋转的性质:旋转前后的三角形全等,即旋转前后的三角形对应线段相等,对应角相等,对应点与旋转中心所连线段的夹角相等。
例 2(2024 巴南区阶段练习改编)如图,$Rt\triangle ABC$ 中,$\angle A = 90^{\circ}$,$\angle ABC = \alpha$,将 $Rt\triangle ABC$ 绕点 $C$ 逆时针旋转得到 $Rt\triangle EDC$,点 $A$ 的对应点 $E$ 正好落在 $BC$ 上,连接 $BD$,则 $\angle CBD$ 的度数是
45°+α/2
。
名师导引 注意运用旋转的性质:旋转前后的三角形全等,即旋转前后的三角形对应线段相等,对应角相等,对应点与旋转中心所连线段的夹角相等。
答案:
45°+α/2
查看更多完整答案,请扫码查看


